Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Roustoucí posloupnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 10. 2012 13:35
Roustoucí posloupnost
Ahoj, mohl by mi někdo prosím objasnit postup výpočtu?
Ukaž že posloupnost je rostoucí: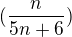
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
- (téma jako vyřešené označil(a) PanTau)
#2 20. 10. 2012 14:30
Re: Roustoucí posloupnost
Ahoj,
definice rostoucí posloupnosti je taková, že následující člen je vždy větší než člen předchozí. To znamená, že ve výsledku bude rostoucí celá - můžeš si třeba zkusit vypsat pár členů :
a vidíš, že 
Potřebujeme tedy dokázat, že: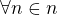 platí
platí 
Uměl bys pokračovat (tj jakoby řešit tuto nerovnici pro n)?
Offline
#3 20. 10. 2012 14:46
Re: Roustoucí posloupnost
↑ Sulfan:
Pokud jsem neudělal chybu tak -


Snad jsem vše naťukal správně. Důležité je, že nahoře mi vyjde -1n-6, podle výsledků má být nahoře POUZE 6
(nahoře=čitatel)
(Výsledek zapsat umím - jen je složité to sem ťukat přes kód)
Asi neumím násobit jednoduchá čísla, nebo kde jsem se seknul? 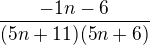
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Roustoucí posloupnost (TOTO TÉMA JE VYŘEŠENÉ)

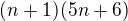 (tj z druhého kroku na třetí krok). Už chybu vidíš?
(tj z druhého kroku na třetí krok). Už chybu vidíš?