Matematické Fórum

xxxxx19

Ahoj, bud implicitni krivka zadana jako

$(x^{2}+y^{2})^{2}=a(x^{3}-3xy^{2})$ kde $a>0$

a počítám obsah vymezený touto křivkou.

položme
$x=rcos(t), y=rsin(t)$

Jakobian je pak $J=r$

Po dosazení
$r^{4}=a(r^{3}cos^{3}(t)-3r^{3}cos(t)sin^{2}(t))$

$r=cos(t)(4cos^{2}(t)-3)^{2}$

A tedy řeším dvojitý integrál:
$\int_{0}^{2\pi }(\int_{0}^{acos(t)(4cos^{2}(t)-3)} (1*r)dr)dt$

Vyřeším jeden:
$\int_{0}^{2\pi }\frac{1}{2}a^{2}cos^{2}(t)(4cos^{2}(t)-3)^{2} dt$

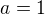A toto vychází numericky vypočteno $\pi /2$ pro $a=1$ ale mát o vyjít pro toto a $\pi /4$

Edit: Je mi jasný že chyba bude někde v mezích, ten integrál budu počítat analyticky až potom co zjistim co je špatně na tom co vidíte, pak vyjádřim obecný vzorec a pro parametr a

xxxxx19 · 21. 10. 2012 11:42

problem?

Brano · 21. 10. 2012 12:17

$r=cos(t)(4cos^{2}(t)-3)^{2}$ tu ti vypadlo $a$ (ale dale ho mas takze OK)

Treba si uvedomit, ze $r\ge 0$ , cize neintegruj $t$ cez $[0,2\pi]$ ale iba cez podmnozinu, kde je $r\ge 0$

Matematické Fórum

#1 20. 10. 2012 13:49 — Editoval xxxxx19 (20. 10. 2012 13:51)

Implicitní funkce - dvojitý integrál

#2 21. 10. 2012 11:42

Re: Implicitní funkce - dvojitý integrál

#3 21. 10. 2012 12:17

Re: Implicitní funkce - dvojitý integrál

Zápatí