Matematické Fórum

etchie · 21. 10. 2012 14:57

pomocou Vennových diagramov nie je problém zistiť, že a) platí b) neplatí

Je možný aj iný postup, bez diagramov ?
A keď chcem pre b) uviesť kontrapríklad, tak ako na to ?

ďakujem za radu

Blackflower · 21. 10. 2012 15:43

Taký nápad - skús si obe rovnice rozpísať na disjunktné množiny, napríklad aj pomocou obrázka.

etchie · 21. 10. 2012 17:33

↑ Blackflower:

čo sú disjunktné množiny (dúfam) viem aj viem urobiť rozklad množiny celých čísel na disjunktné množiny pomocou zvyškových tried. no tu sa mi to ďalej s ničím nespája.

napísal som si takýto rozklad:
$(X \cap Y \cap Z) \cup (X-Y-Z) \cup (Y-X-Z) \cup (Z-X-Y) \cup (X \cap Y-Z) \cup (X \cap Z-Y) \cup (Y \cap Z-X)$
ale neviem, čo s tým, ani či v tom je nejaký zmysel

etchie · 22. 10. 2012 22:23

stále neviem, čo s tým kontrapríkladom.
kontrapríklady sa dajú robiť keď sa negujú výroky. a tu potrebujem negovať množiny, čo by sa dalo, ak by bola definovaná nejaká základná množina. ale nie je.

Fabo · 22. 10. 2012 22:34

Tak v principe ide o vyrok, ze pre kazde X, Y, Z pre ktore dany vzorec dava zmysel, plati tento vzorec, resp. aspon ja to tak vidim. Kontrapriklad, postupujes podobne ako pri vyrokoch, existuje aspon jedna skupina mnozin X, Y, Z, pre ktore rovnica neplati, a das priklad, ja neviem, X nech je {1,2,3} Y nech je {1} a Z {2}

kompik · 23. 10. 2012 12:13

etchie napsal(a):
Je možný aj iný postup, bez diagramov ?

Overit, ci $X\cap(Y-Z)=(X\cap Y)-(X\cap Z)$ vlastne znamena overit
$$$$ x\in X\cap(Y-Z) \Leftrightarrow x\in (X\cap Y)-(X\cap Z) $$$$

Skusme prepisat lavu a pravu stranu zvlast:
$x\in X\cap(Y-Z) \Leftrightarrow (x\in X) \land (x\in Y-Z) \Leftrightarrow (x\in X) \land (x\in Y) \land (x\notin Z)$

$x\in (X\cap Y)-(X\cap Z) \Leftrightarrow (x\in X\cap Y) \land \neg (x\in X\cap Z) \Leftrightarrow (x\in X \land x\in Y) \land \neg (x\in X \land x\in Z) \Leftrightarrow (x\in X) \land (x\in Y) \land (x\notin X \lor x\notin Z)$

Ak si oznacim $p\equiv (x\in X)$ , $q\equiv (x\in Y)$ a $r\equiv(x\in Z)$ , tak sme lavu stranu prepisali na $p\land q\land \neg r$ a pravu stranu na $p\land q \land (\neg p \lor \neg r)$ . Cize staci skontrolovat ze $p\land q\land \neg r \Leftrightarrow p\land q \land (\neg p \lor \neg r)$ je tautologia.

Poznamka Ked sa nad tym clovek trochu zamysli, tak Vennove diagramy a tabulky na overenie tautologie su v podstate to iste - mame tam jednu oblast/jeden riadok pre kazdu kombinaciu true/false; v jednom pripade vysrafujeme oblasti kde to plati, v druhom piseme jednotky a nuly.

Pozri tento obrazok:

z Wikipedie.

etchie napsal(a):
A keď chcem pre b) uviesť kontrapríklad, tak ako na to ?

Ked si si nakreslil diagram, tak z neho vidis, ze na najdenie kontkretneho kontraprikladu ti stacia akekolvek mnoziny, take ze tam mas prvky v 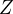$Z$ , ktore nie su v $X$ ani v $Y$ .

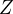Napriklad $X=Y=\emptyset$ a $Z=\{\emptyset\}$ . (Resp. za $Z$ tu mozes zobrat hocijaku neprazdnu mnozinu.)