Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 11. 2008 20:05 — Editoval matoxy (22. 11. 2008 20:06)
Aproximácia funkcie polynómom
Pekný zasnežený:) sobotný večer.
Mal by som takú otázku: Ak chceme približne nahradiť nejakú funkciu polynómom, platí vzorec:  . Ak sa nemýlim tak to vyplíva z toho, že keď derivujeme polynóm n-krát a uvažujeme x=0, tak pri a_n vždy x derivovaním "vypadne", ale prečo mi vlastne funkciu derivujeme? Viem, že nám to tak pekne vychádza, ale nemalo by to nejaké logické vysvetlenie?
. Ak sa nemýlim tak to vyplíva z toho, že keď derivujeme polynóm n-krát a uvažujeme x=0, tak pri a_n vždy x derivovaním "vypadne", ale prečo mi vlastne funkciu derivujeme? Viem, že nám to tak pekne vychádza, ale nemalo by to nejaké logické vysvetlenie?
+Takýmto spôsobom môžeme pre funkciu sin x dostať istý vzorec. Našiel som ho aj na wikipédii, ale prečo je tam napísané, že je tým radom definovaná v komplexných číslach? Platí to predsa aj normálne s reálnymi nie?
You know who
(or maybe not)
Offline
#2 23. 11. 2008 14:31 — Editoval Pavel (24. 11. 2008 08:06)
Re: Aproximácia funkcie polynómom
↑ matoxy:
- zřejmě používáš Taylorův rozvoj, pak ale platí  .
.
- výhoda spočívá v tom, že se polynomy se mnohem lépe pracuje (např. při integrování, počítání limit, atd.) než s obecnými nepolynomickými funkcemi. Proto se často využívá toho, že funkci, která splňuje předem dané požadavky, lze s libovolnou přesností polynomem nahradit.
- pokud něco platí v komplexních číslech, tím lépe. Pak to platí také v reálném oboru.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 23. 11. 2008 19:07 — Editoval matoxy (23. 11. 2008 19:08)
Re: Aproximácia funkcie polynómom
Pavel, nevedel som, že sa to volá Taylorov rozvoj. Pred dvoma týždňami som bol totiž na jednej prednáške, kde sa rozprávalo o aproximácii funkcií polynómami a vtedy som mal aj pocit, že som to pochopil. Teraz mi už bolo čosi nejasné, no už som si ozrejmil ako dostaneme tento vzorec: (aspoň podľa mojich poznámok z prednášky je to tak).
(aspoň podľa mojich poznámok z prednášky je to tak).
Napíšem sem to odvodenie, len že či to dobre chápem:
1.)
Predpokladajme, že nejaká funkcia f(x) sa dá "preložiť" polynómom  .
.
v bode x=0 bude platiť 
2.)
a_1 potom dostaneme tak, že zderivujeme funkciu a vypočítame funkčnú hodnotu v nule, teda 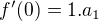
Pre a_2 dostaneme 
Všeobecne teda môžeme písať, že 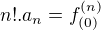 , čo je ten vzťah, ktorý si napísal ty.
, čo je ten vzťah, ktorý si napísal ty.
Moja otázka však smerovala hlavne k tomu, prečo sme vlastne v druhom kroku derivovali polynóm? Má to nejaké logické odvôvodenie okrem toho, že sme tým dostali to čo sme chceli?
- k tým komplexným číslam. Konkrétne pre funkcii sin x to má nejakú špeciálnu výhodu, že to platí aj v komplexných číslach.
You know who
(or maybe not)
Offline
#4 23. 11. 2008 19:45 — Editoval Olin (23. 11. 2008 19:47)
Re: Aproximácia funkcie polynómom
Vem to tak, pokud se mají (přibližně) rovnat funkční hodnoty ve všech bodech, musí se ve všech (přibližně) rovnat i jeho derivace (první i vyšších řádů).
To znamená, jestliže ty máš nějaký polynom 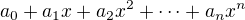 , tak jeho hodnota je pro x=0 rovna
, tak jeho hodnota je pro x=0 rovna  . Když ten polynom zderivujeme, tak nám zmizí
. Když ten polynom zderivujeme, tak nám zmizí  a absolutním členem je
a absolutním členem je  . Při dosazení x=0 "zmizí" všechny členy až na absolutní, takže derivace v nule bude
. Při dosazení x=0 "zmizí" všechny členy až na absolutní, takže derivace v nule bude  . Když derivujeme ještě jednou, bude absolutním členem
. Když derivujeme ještě jednou, bude absolutním členem 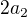 , opět při dosazení nuly zbyde jen tento absolutní člen. Obecně se snažíme o to, aby pro x=0 platilo
, opět při dosazení nuly zbyde jen tento absolutní člen. Obecně se snažíme o to, aby pro x=0 platilo
pokud možno až po co nejvyšší k (v případě Taylorovy řady až do nekonečna).
Offline
#5 24. 11. 2008 00:37 — Editoval lukaszh (24. 11. 2008 00:37)
Re: Aproximácia funkcie polynómom
↑ matoxy:
Ahoj, popíšem postup odvodenia Taylorovho polynómu. Tak laicky :-)
Vezmi si najprv takú myšlienku, že dve funkcie sú "rovnaké" (v istom zmysle) ak sa rovnajú ich všetky derivácie. Teda prvá derivácia jednej sa rovná prvej derivácii druhej funkcie, atď. Teraz hľadáme taký polynóm  aby v bode 0 čo najlepšie aproximoval hodnoty funckie
aby v bode 0 čo najlepšie aproximoval hodnoty funckie  . Nech
. Nech  je polynóm n-tého stupňa. Má teda platiť, že
je polynóm n-tého stupňa. Má teda platiť, že 
Tie derivácie si môžem ekvivalentne prepísať nasledovne:
Veľmi dôležitým poznatkom je práve posledná rovnosť, ktorá znamená, že keď x^n, n-krát zderivuješ dostaneš n!.
Dosadením x = 0 dostaneš koeficienty a_1, a_2, atd
Teraz ti už len zostáva vyjadriť koeficienty: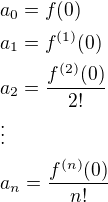
A teda výsledný polynóm bude mať tvar: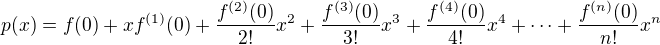
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 24. 11. 2008 17:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aproximácia funkcie polynómom
Zdravím vás :-)
přidám ještě hezkou ukazku z tradičnich zdrojů
-----------
"jste příliš skromný, pane Maříku, ale já zase vím, že jste příliš velký umělec, než abyste se dnes nedal slyšet...zahrejte nám. Nemusíte hrár ani Bacha, ani Haydna, ani Chopina, zahrejte nám jednu ze svích improvisaci..."
Offline

