Matematické Fórum

SoniCorr

Zdravím, potřeboval bych zkontrolovat nasledujici vyroky.

Pro každé nezáporné celé číslo x platí, že k tomu, aby x=0, stačí, aby x<1.

$(\forall x\in Z, x>0)((x<0)\Leftrightarrow (x=0))$

Kdykoliv jsou realna cisla a,b taková, ze plati a+b=1. pak alespon jedno z nich je vetsi nebo rovno 1/2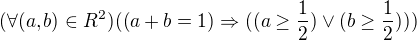

$(\forall (a,b)\in R^2)((a+b=1)\Rightarrow ((a\ge \frac{1}{2})\vee (b\ge \frac{1}{2})))$

Pro kazde realne cislo x, pro ktere x>1, plati x^2-1>0
$(\forall x\in R,x>1)(x^2-1>0)$

Pro kazde realne cislo x plati, ze je-li 1/x<1,pak odtud neplyne 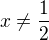$x\not =\frac{1}{2}$
$(\forall x\in R)((\frac{1}{x}<1)\Rightarrow (x=\frac{1}{2},x=\emptyset ))$

Pro vsechny dvojice realnych cisel x,y plati : je-li x+=2 a y>=x, pak take 1>=x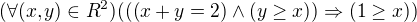

$(\forall (x,y)\in R^2)(((x+y=2)\wedge (y\ge x))\Rightarrow (1\ge x))$

Je-li x libovolne realne cislo, pak existuje prirozene cislo n tak, ze plati n>x

$(\forall x\in R)\Rightarrow ((\exists n\in N)(n>x))$

Pro kazde realne cislo x plati, ze ze skutecnosti, ze x je ruzne od nuly, plyne, ze x^2=2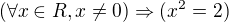
$(\forall x\in R,x\not =0)\Rightarrow (x^2=2)$

Pro vsechna cela cisla x plati, ze neni-li x sude, neni ani liche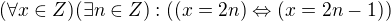

$(\forall x\in Z)(\exists n\in Z):((x=2n)\Leftrightarrow (x=2n-1))$

A tento výrok nevím : není pravda, ze pro kazde realne cislo x je x^2>0. Napisu si to bez toho neni pravda a zneguji to?

etchie · 23. 10. 2012 20:52 — Editoval etchie (23. 10. 2012 20:56)

tento sa mi nepáči:
$(\forall x\in R)((\frac{1}{x}<1)\Rightarrow (x=\frac{1}{2},x=\emptyset ))$
skôr by malo byť:
$(\forall x\in R)((\frac{1}{x}<1)\Rightarrow (x =\frac{1}{2}))$

ostatné pred ním ok, za ním som nekontroloval

Edit: aha, tak nie. je to dobre. iba tá prázdna množina asi má znamenať že x <> 0

SoniCorr · 23. 10. 2012 22:04

Jeste me napadlo, ze bych napsal jakoze z toho plyne a pak znegoval pouze zavorky (ne negaci implikace)

Brano · 23. 10. 2012 22:52 — Editoval Brano (23. 10. 2012 23:00)

Nie som stastny z pisania rieseni, ale k tomuto fakt neviem vymysliet navod, pride mi to ako pravopis to sa proste treba naucit, ale bolo by dobre si skusit poriadne po sebe precitat co ten formalny zapis hovori.

1. $(\forall x\in Z, x\ge 0)((x<1)\Rightarrow(x=0))$
2. ok
3. ok
4. $(\forall x\in R)\neg((\frac{1}{x}<1)\Rightarrow (x=\frac{1}{2}))$
(ta negacia by sa sice dala upravit, ale zda sa mi, ze zadanie neziada najst najjednoduchsi ekvivalentny zapis, ale zapis co najblizsi tej vete v prirodzenom jazyku)
5. asi ok, preklep je zrejme v zadani
6. $(\forall x\in R)((\exists n\in N)(n>x))$
Nema zmysel pouzivat operaciu medzi kvantifikatorom a vyrokovou formou, operacie su platne medzi vyrokmi, alebo vyrokovymi formami. Ak tam velmi chces tu implikaciu tak potom takto.
$(\forall x)[( x\in R)\Rightarrow(\exists n\in N)(n>x)]$ ... vidis rozdiel?
7. Znova to iste
bud $(\forall x\in R)[(x\not =0)\Rightarrow (x^2=2)]$ alebo $(\forall x\in R,x\not =0)(x^2=2)$
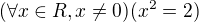
8. $(\forall x\in Z)(\neg[(\exists n\in Z)(x=2n)]\Rightarrow \neg[(\exists n\in Z)(x=2n-1)])$

pozn. k "citaniu"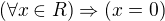
$(\forall x\in R)\Rightarrow (x=0)$ by sa precitalo: pre kazde realne x potom x je rovne 0 ... trochu divne, nie?
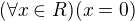$(\forall x\in R)(x=0)$ ... pre kazde realne x je x rovne 0
$(\forall x)[(x\in R)\Rightarrow (x=0)]$ ... pre kazde x (plati) ak x je realne potom x je rovne 0

este jedna poznamka:
mozno netreba tak vydatne zatvorkovat ako to robim ja, ale kedze nemam cit pre priority logickych operatorov ako mam napr. pre +, -, *, /, tak si chcem byt isty, ze je to dobre.

kexixex · 24. 10. 2012 18:58

↑ SoniCorr:

taky neni dobry psat neco jako : 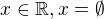$x\in \mathbb{R},x=\emptyset$ , protoze x je prvek mnoziny realnych cisel a ne mnozina

k otazce na konci: Ano, staci napsat vyrok, dat ho do zavorky a pred nej negaci..

SoniCorr · 25. 10. 2012 09:04

takze takhle : $\neg[(\forall x\in R)(x^2>0)]$ ?

Matematické Fórum

#1 23. 10. 2012 17:59 — Editoval SoniCorr (23. 10. 2012 18:01)

další výroky

#2 23. 10. 2012 20:52 — Editoval etchie (23. 10. 2012 20:56)

Re: další výroky

#3 23. 10. 2012 22:04

Re: další výroky

#4 23. 10. 2012 22:52 — Editoval Brano (23. 10. 2012 23:00)

Re: další výroky

#5 24. 10. 2012 18:58

Re: další výroky

#6 25. 10. 2012 09:04

Re: další výroky

Zápatí