Matematické Fórum

drabi · 24. 10. 2012 21:06

Ahoj, mám problém ještě s tímto příkladem, mám dokázat, že pro libovolné 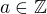$a \in \mathbb{Z}$ a každá dvě různá prvočísla $p,q$ platí: $pq|a^{p+q} - a^{p+1} - a^{q+1} + a^{1+1}$

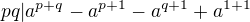
Moc jsem s tím zatím moc nehla, pouze jsem to převedla na tvar 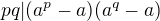$pq| (a^p - a)(a^q-a)$

Mohl by mě prosím někdo nějak navést? Díky

o.neill · 24. 10. 2012 21:08

Jestli to máš upraveno správně, tak z toho čuchám Malou Fermatovu větu.

drabi · 24. 10. 2012 21:25

↑ o.neill:
hmm, tak to bude asi třeba rozdělit na více případů:
(a) 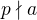$p\nmid a$ & $q \nmid a$
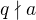
(b) 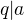$p\nmid a$ & $q | a$ resp. $q\nmid a$ & $p | a$
(c) $pq | a$

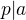
(c) je jasné, tam pak není co řešit
(b) je vlastně jedna část (a) tedy, že 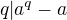$q | a^q - a$ resp. $p | a^p - a$
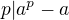
takže mám
$a^q - a \equiv 0 \text{mod} q$
$a(a^{q-1} - 1) \equiv 0 \text{mod} q$ a jelikož 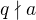$q \nmid a$ , tak dle malé Fermatovy věty máme, že 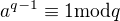$a^{q-1} \equiv 1 \text{mod} q$ což nám dává, že $a\cdot 0 \equiv 0 \text{mod}q$ což platí.
Obdobně pro $p$
Je to tak?

o.neill · 24. 10. 2012 22:04

No asi bych to šlo udělat trochu jednodušeji. Malá Fermatova věta se dá taky upravit do tvaru 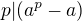$p|(a^p-a)$ , a to i bez předpokladu, že 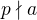$p\nmid a$ , neboť pokud $p|a$ , tak to platí celkem zjevně. No a pak už je to dokázat triviální a ani se to nemusí rozdělovat na žádné případy.

drabi · 24. 10. 2012 22:05

↑ o.neill:
jo máš nejspíš pravdu:) Každopádně díky za pomoc

Matematické Fórum

#1 24. 10. 2012 21:06

dělitelnost

#2 24. 10. 2012 21:08

Re: dělitelnost

#3 24. 10. 2012 21:25

Re: dělitelnost

#4 24. 10. 2012 22:04

Re: dělitelnost

#5 24. 10. 2012 22:05

Re: dělitelnost

Zápatí