Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 10. 2012 15:03
Odmocniny
Ahoj. Potřeboval bych vysvětlit a poradit, jak se počítají tyto příklady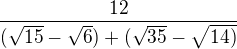
Paní profesorka nic nevysvětlí a počítá si to na tabuli dá se říct jen pro sebe. Nechápu třeba, kde pak ve výpočtu bere některá čísla. Byli by jste moc hodní, kdyby jste mi poradili.
Quidquid latine dictum sit, altum videtur - Cokoli je řečeno latinsky, vypadá vznešeně.
Offline
- (téma jako vyřešené označil(a) Janisek)
#4 25. 10. 2012 15:52
Re: Odmocniny
Ne. Zlomek upravíme výše uvedeným postupem (psal jsem jen jmenovatele) na  Potom rozšíříme zlomek takovým výrazem, aby nám zmizely odmociny ze jmenovatele. Hodí se ta to vzorec
Potom rozšíříme zlomek takovým výrazem, aby nám zmizely odmociny ze jmenovatele. Hodí se ta to vzorec 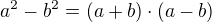
Doučím M, Ch v okolí Pardubic
Press any key to continue. Alt + F4?
Offline
#14 25. 10. 2012 21:50
Re: Odmocniny
Děkuji.
K dalšímu studiu vřele doporučuji sbírku od J. Kubáta (taková růžová), tam jsou některé věci i vysvětleny. V nejhorším případě je tady J. Petáková. A ZDE jsem našel pár příkladů ve Wordu (.doc), formátování maj sice hrozný, ale na tom zas tak nesejde.
Doučím M, Ch v okolí Pardubic
Press any key to continue. Alt + F4?
Offline



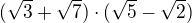 a vyjde
a vyjde 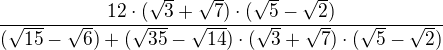 ? A pak to jen roznásobím?
? A pak to jen roznásobím?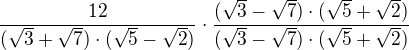
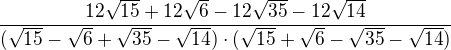 ?
?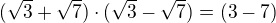
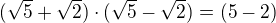
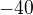 a v čitateli těch
a v čitateli těch  ?
? Mohu to nějak zkracovat? Nebo jak bude vypadat další postup?
Mohu to nějak zkracovat? Nebo jak bude vypadat další postup?
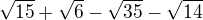 A je to určitě správně? Zadání se výsledku až moc podobá :D
A je to určitě správně? Zadání se výsledku až moc podobá :D