Matematické Fórum

Google · 28. 10. 2012 09:05

Zdravím, muj příklad je:

Dokazují se 2 body, že ano?:

Nejdříve musím vyřešit $\frac{(-1)^{n}(2n-1)}{3n-5}\ge -5/4$ . Problemem je ze nevim jak.
Zkousel jsem to takto: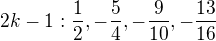
$2k-1: \frac{1}{2},-\frac{5}{4},-\frac{9}{10},-\frac{13}{16}$
$2k: 3,1,\frac{11}{3},\frac{15}{19}$
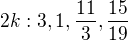
Z toho vyčtu členu vidím, že -5/4 je minimum.
Ale Predpokladam že zpusob ktery jsem pouzil by nebyl u zkousky nebo v pisemce připustný.
Mohl by mi někdo řict jak na to?

Mám ještě jednu otázku: A potom kdybych dokazal bod 1. A take dokazal že infimum je zaroveň minimum, znamená to, že nemusím dokazovat bod 2?
Děkuju

o.neill

Včera jsem to počítal :D

Jenom trochu k pojmům. -5/4 rozhodně není minimum. Minimum množiny je nejmenší prvek a -5/4 do této množiny nenáleží. Tato množina minimum nemá, ovšem je pravda, že můžeme najít prvek libovolně blízký -5/4, avšak není zde žádný menší a této vlastnosti se neříká minimum, ale právě infimum.

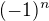No a teď jak dokázat tu první vlastnost a tedy to, že neexistuje žádný menší prvek, tedy $\frac{(-1)^{n}(2n-1)}{3n-5}\ge -5/4$ . Když je ve vzorci $(-1)^n$ , tak se s tím počítá dost blbě takže je dobré si to rozdělit na n lichá a n sudá. Pro n sudá přirozená (tedy tím větší než dva) je výraz vlevo rozhodně kladný, a tedy větší než -5/4. Pro n lichá máme 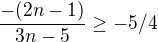$\frac{-(2n-1)}{3n-5}\ge -5/4$ , což je normální nerovnice. Jestliže všechna lichá kladná čísla jsou jejími kořeny, pak máme dokázáno.

Druhou vlastnost je třeba dokázat obdobně. Hledáme n takové, aby $\frac{(-1)^{n}(2n-1)}{3n-5}<-5/4+\varepsilon$ pro každé $\varepsilon>0$ . Mezi n sudými je hledat nesmysl, protože to víme, že ta levá strana je kladná a pravá je pro malá epsilon záporná, a tak budeme hledat jenom mezi lichými.