Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » de Morganova pravidla (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 10. 2009 15:43
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
de Morganova pravidla
Dobrého odpoledne přeji,
je v tom nějak zakopaný pes, už asi hodinu se snažím nějak matematicky dokázat jedno z de M. pravidel. Jedno bylo v pohodě, druhé nějak ne a ne vyjádřit.
Zadání:
Mějme množiny  , kde
, kde  Pak platí:
Pak platí:
(nějak neumím vysázet rozdíl množin)
Asi by se to mělo dokazovat přes oboustrannou inkluzi, případně jen jednostrannou s ekvivalentními kroky - takže nebude té druhé třeba (resp. bude se pouze číst "odzadu"). Chtěl jsem nějak začít, ale nevím, jak ty množiny vyjádřit.
Návody na internetu jsem četl, ale nějak z toho nejsem chytrej. Došel jsem akorát k tomuto:
Beru libovolný prvek z levé strany. Patří do S ( ) a zároveň nepatří do průniku, takže nenáleží do A_1 nebo do A_2 nebo do A_3, ..., takže patří do sjednocení doplňků
) a zároveň nepatří do průniku, takže nenáleží do A_1 nebo do A_2 nebo do A_3, ..., takže patří do sjednocení doplňků  , pokud to tedy patří do S i do tohoto sjednocení, patří to do
, pokud to tedy patří do S i do tohoto sjednocení, patří to do 
Je to nějaké kostrbaté a hlavně ten první úkon (průnik -> doplněk) bych u zkoušky asi nějak neobhájil logicky.
Teď na to s odstupem několika minut koukám a nejspíš to zní i logicky, proto bych rád nějaké komentáře/rady, jak nějak ten důkaz zaonačit, děkuji.
Offline
#2 29. 10. 2009 16:17 — Editoval BrozekP (29. 10. 2009 23:35)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: de Morganova pravidla
Pokud tomu dobře rozumím, tak doplňkem myslíš doplňek do množiny  , tedy
, tedy 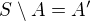 . Pak ale nechápu
. Pak ale nechápu
pokud to tedy patří do S i do tohoto sjednocení, patří to do
.
to je pak automaticky splněno, když je to to samé.
Místo formulací "patří do ... nebo do ... nebo do ..." bych volil formulaci "existuje  takové, že
takové, že  ". Takže celý důkaz by vypadal takto:
". Takže celý důkaz by vypadal takto:
Nechť  .
.  je tedy prvkem
je tedy prvkem  a není prvkem
a není prvkem  , existuje tedy
, existuje tedy  takové, že
takové, že  . To znamená, že
. To znamená, že  je prvkem
je prvkem  a tedy i prvkem sjednocení
a tedy i prvkem sjednocení 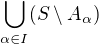 .
.
Opačně nechť  . Existuje tedy
. Existuje tedy  takové, že
takové, že  . To ale znamená, že
. To ale znamená, že  . Nemůže proto být ani prvkem průniku
. Nemůže proto být ani prvkem průniku  . Proto musí být prvkem
. Proto musí být prvkem  .
.
Edit: Ještě upozornění - nikde se neřeklo, že  je spočetná množina, nemůžeš tedy obecně vyjmenovat všechny
je spočetná množina, nemůžeš tedy obecně vyjmenovat všechny  jako
jako 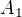 ,
, 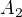 ,
, 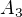 , ...
, ...
Offline
#3 28. 10. 2012 11:14 — Editoval nakoolla (28. 10. 2012 11:15)
Re: de Morganova pravidla
↑ Pavel Brožek: mohla bych se, prosím, zeptat, jak se v tom důkazu vzalo to  a proč nemůže být x ani prvkem průniku? Snažila jsem se to i nakreslit, ale nějak to nechápu. Díky moc.
a proč nemůže být x ani prvkem průniku? Snažila jsem se to i nakreslit, ale nějak to nechápu. Díky moc.
Offline
#4 28. 10. 2012 11:31 — Editoval Pavel Brožek (28. 10. 2012 11:31)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: de Morganova pravidla
↑ nakoolla: je označení pro ten index, pro který platí
je označení pro ten index, pro který platí  . Mohl jsem ho klidně označit jinak, to prostě byla moje volba značení.
. Mohl jsem ho klidně označit jinak, to prostě byla moje volba značení.
Kdyby x bylo prvkem  pak přece nemůže být prvkem
pak přece nemůže být prvkem 
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » de Morganova pravidla (TOTO TÉMA JE VYŘEŠENÉ)
