Matematické Fórum

xxxxx19 · 28. 10. 2012 10:19

Ahoj,
Zkoumám implicitní křivku $\sqrt[y]{x}=\sqrt[x]{y}$

kolem $x=y=0,007$ dojde k jakémusi "rozdvojení", nevíte někdo jestli se jedná o nějakou speficikou hodnotu.

K podobnému rozvětvení dochází i u $[\frac{1}{e},\frac{1}{e}]$

Code:

<< Graphics`ImplicitPlot`;
ImplicitPlot[x^(1/y) == y^(1/x), {x, 0, 0.02}, {y, 0, 0.02}]

Díky za nápady.

Pavel Brožek

↑ xxxxx19:

Ahoj,

přikládám obrázek, aby i ostatní měli představu, o čem se bavíme:

zápis $\sqrt[y]{x}=\sqrt[x]{y}$ můžeme ekvivalentně přepsat jako $x^x=y^y$ . Když si vyšetříš průběh funkce $f(x)=x^x$ , zjistíš, že klesá z 1 v $x=0$ k $\mathrm{e}^{-\frac1{\mathrm{e}}}$ v $x=\frac1{\mathrm{e}}$ a pak roste do nekonečna.

Podívejme se na množinu bodů splňujících $x^x=y^y=c$ , kde $c\in\[\mathrm{e}^{-\frac1{\mathrm{e}}},\infty\)$ je pevně dané. Pro $c=\mathrm{e}^{-\frac1{\mathrm{e}}}$ dostaneme jediný bod $\[\frac1{\mathrm{e}},\frac1{\mathrm{e}}\]$ . Pokud začneme zvětšovat c, mohou nastat 4 možnosti kam se budeme v rovině xy pohybovat po té implicitní křivce:

1) x=y, x a y s c rostou,
2) x=y, x a y s c klesají,
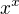3) x klesá, y roste, tato „větev“ skončí při $c=1$ , protože x=0 a už nemá kam klesat, aby $x^x$ mohlo nabývat větších hodnot než 1,
3) x roste, y klesá, tato „větev“ skončí také při $c=1$ , protože y=0 a už nemá kam klesat, aby $y^y$ mohlo nabývat větších hodnot než 1.

Hodnota 0,007 není ničím významná a není důvod, aby tam docházelo k nějakému větvení. Je patrné, že ten graf je špatně, protože neukazuje křivku x=y vedoucí do počátku, ta přitom jistě je součástí implicitní křivky. Půjde tedy o chybné zobrazení Mathematicou. Tomu také napovídá „zubatost“ křivky.

Brano · 28. 10. 2012 11:17

Zapis tvojej krivky by bolo dobre si trochu upravit a to tak, ze rovnost zlogaritmujeme a upraceme na jednu stranu. Dostaneme $f=\frac{\ln x}{y}-\frac{\ln y}{x}=0$ .
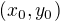Pamatas na vetu o implicitnej funkcii? Hovori, ze aby sa dalo $y$ vyjadrit pomocou $x$ v okoli nejakeho bodu $(x_0,y_0)$ tak musi platit $\frac{\partial f}{\partial y}(x_0,y_0)\not=0$ . Podobne pre $x$ . Z toho si mozme vsimnut, ze problematicke body budu tie, kde sa ani $y$ neda vyjadrit pomocou $x$ ani $x$ pomocou $y$ a to budu riesenia
$\frac{\partial f}{\partial x}=0$ a $\frac{\partial f}{\partial y}=0$
po upravach
$y\ln y+x=0$ a $x\ln x+y=0$ .
Jedno riesenie je uz spominane $x=y=1/e$ . Na najdenie toho druheho (a zistenie, ze to uz je vsetko) si najprv mozes nakreslit tie funkcie a potom si najst nejaku numericku metodu, mal by ti presne vyjst ten bod "rozdvojenia" na ktory si sa najprv pytal.

Brano · 28. 10. 2012 11:35 — Editoval Brano (28. 10. 2012 11:38)

↑ Pavel Brožek:
no zase nerozmyslam poriadne - isteze je jednoduchsie vysetrovat $f=x\ln x-y\ln y(=0)$ . Z coho dostaneme rovnice
$\ln x+1=0$ a $\ln y+1=0$ ktore maju jedine riesenie $x=y=1/e$ .
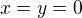To druhe rieseie $y\ln y+x=0$ a $x\ln x+y=0$ uz teraz viem, ze bolo $x=y=0$ a to sa tu vytratilo kvoli nasobeniu 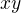$xy$ , ale aj tak to bude vyznamny bod, lebo "problem" s vyjdrovanim nastane aj ak je derivacia nekonecna, nie len nulova. Cize $x=0.007$ je len nepresnost numeriky.

Pavel Brožek

Jen pro úplnost, správně ta implicitní křivka (spíš bych měl asi říkat implicitně zadaná množina bodů) vypadá takto:

xxxxx19 · 28. 10. 2012 12:58

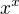funkci $x^{x}$ znam, koukam ze to s timhle souvisi. diky za prispevky. jinak ta numerika blbne i na ipadu aplikace quickgraph, je to tam uplne stejne spatne, zrejme uz je na tak male cislo kratka mantisa.

Matematické Fórum

#1 28. 10. 2012 10:19

"Rozdvojení" implicitní funkce blízko u nuly

Code:

#2 28. 10. 2012 11:17 — Editoval Pavel Brožek (28. 10. 2012 11:21)

Re: "Rozdvojení" implicitní funkce blízko u nuly

#3 28. 10. 2012 11:17

Re: "Rozdvojení" implicitní funkce blízko u nuly

#4 28. 10. 2012 11:35 — Editoval Brano (28. 10. 2012 11:38)

Re: "Rozdvojení" implicitní funkce blízko u nuly

#5 28. 10. 2012 11:41 — Editoval Pavel Brožek (28. 10. 2012 11:42)

Re: "Rozdvojení" implicitní funkce blízko u nuly

#6 28. 10. 2012 12:58

Re: "Rozdvojení" implicitní funkce blízko u nuly

Zápatí