Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2012 20:46
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Relace: důkaz
Ahoj,
mohli byste prosím poradit?
Necht’ R a S jsou relace na konečné množině M a  je relace identity na M.
je relace identity na M.
Jestliže R ° S =  , pak R ° S = S ° R. Dokažte.
, pak R ° S = S ° R. Dokažte.
Rozhodněte, zda uvedená implikace platí i pokud je M nekonečná.
Nebrali jsme bohužel na gymplu důkazy, tak nevím, jak to dokázat. Jak to srozumitelně pak zapsat ?
Ani tedy pořádně nerozumím zadání... :(
Díky za cokoliv, uvítám i literaturu, jiné materiály.
Offline
#2 28. 10. 2012 21:43 — Editoval kompik (28. 10. 2012 21:45)
Re: Relace: důkaz
Neviem, ci to budem vediet dobre vysvetlit - dost by pomohlo kreslit obrazky. (Mozno sa to da dokazat aj nejako jednoduchsie, ako sa tu snazim vysvetlit.)
V prvom rade treba rozumiet tomu ako funguje skladanie relacii.
Je to podobne ako skladanie funkcii, ten obrazok na Wikipedii dava celkom nazornu predstavu - jednoducho sa pozeras, kam sa mozes z daneho bodu dostat po sipkach. Rozdiel medzi relaciami a funkciami je, ze pre funkcii ide z kazdeho bodu prave jedna sipka, pri relacii ich moze ist viac ale nemusi aj ziadna.
V tomto pripade ide o relacie na mnozine  , co znamena
, co znamena  . (Dva prvky x, y su v zlozenej relacii ak sa cez nejake z viem dostat z x do z po "S-kovej" sipke a zo z do y po "R-kovej sipke").
. (Dva prvky x, y su v zlozenej relacii ak sa cez nejake z viem dostat z x do z po "S-kovej" sipke a zo z do y po "R-kovej sipke").
V zadani mame, ze  . (Myslim, ze tu mas preklep v tom, co si napisal.) Zname na to teda, ze vsetky dvojice tvaru
. (Myslim, ze tu mas preklep v tom, co si napisal.) Zname na to teda, ze vsetky dvojice tvaru  su v zlozenej relacii teda pre kazde x musi existovat nejake z tak, ze
su v zlozenej relacii teda pre kazde x musi existovat nejake z tak, ze  .
. .
.
Pre kazde  si oznacme ako
si oznacme ako  mnozinu takych
mnozinu takych  .
. .
.
Zatial sme si vsimli, ze kazde  je neprazdna mnozina, ma teda aspon jeden prvok.
je neprazdna mnozina, ma teda aspon jeden prvok.
Skusme sa este zamysliet nad tym, ci pre rozne prvky mozu mat tieto dve mnoziny neprazdny prienik.
Ak by platilo  , tak mame
, tak mame  a sucasne
a sucasne  . Z toho vyplyva
. Z toho vyplyva  . Lenze zlozena relacia je identita, cize neobsahuje ziadne ine dvojice ako dvojice, kde su obe suradnice rovnake. To teda znamena, ze
. Lenze zlozena relacia je identita, cize neobsahuje ziadne ine dvojice ako dvojice, kde su obe suradnice rovnake. To teda znamena, ze 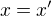 .
.
Prave sme teda ukazali
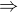
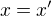 ,
,
inak povedane, pre rozne prvky  a
a 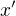 su mnoziny
su mnoziny  a
a  disjunktne.
disjunktne.
Mame teda system mnozin  , je ich tolko, kolko je prvkov mnoziny
, je ich tolko, kolko je prvkov mnoziny  , kazda je neprazdna. Cize z toho vidime, ze kazda takato mnozina musi byt jednoprvkova a spolu pokryju celu mnozinu
, kazda je neprazdna. Cize z toho vidime, ze kazda takato mnozina musi byt jednoprvkova a spolu pokryju celu mnozinu  . (Tu sme vyuzili, ze mnozina je konecna.)
. (Tu sme vyuzili, ze mnozina je konecna.)
Teda aj obratene, kazde  sa dostane prave do jednej takej mnoziny; inak povedane, pre kazde
sa dostane prave do jednej takej mnoziny; inak povedane, pre kazde  existuje prave jedno
existuje prave jedno  take ze
take ze  .
.
Mame teda: 
To znamena, ze  . Vidime teda, ze
. Vidime teda, ze  .
.
Ak by do  patrila nejaka dvojica ineho tvaru, teda nejaka dvojica
patrila nejaka dvojica ineho tvaru, teda nejaka dvojica  taka, ze
taka, ze  , znamenalo by to, ze existuje
, znamenalo by to, ze existuje  take, ze:
take, ze:
Pre 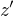 mame prave jedno
mame prave jedno 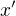 take, ze
take, ze  . Podobne pre
. Podobne pre  mame prave jedno
mame prave jedno 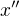 take, ze
take, ze  . Toto konkretne znamena:
. Toto konkretne znamena: ;
; .
.
Kombinaciou tychto veci dostaneme  a
a  ; co znamena
; co znamena  .
.
Sucasne vieme, ze tieto dva prvky su rozne,  . (Lebo pre kazde
. (Lebo pre kazde  mame prave jedno
mame prave jedno  .) Dostali sme spor.
.) Dostali sme spor.
Teda ine dvojice tam uz patrit nemozu.
Zaver:  .
.
******
Pre nekonecne mnoziny to nemusi platit, staci zobrat  a relacie
a relacie  a
a  .
.
Offline
#3 28. 10. 2012 22:35
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Re: Relace: důkaz
↑ kompik:
Mockrát děkuji za tak vyčerpávající odpověď, zkusím si to ve své hlavě přeložit do lehce nematematického jazyka, snad to bude ok :)
Čímž zároveň nechávám prostor pro ostatní, kdyby to chtěli nějakým způsobem přetransformovat a dát jak tady kompikovi, tak i mě jiný pohled na věc :)
jinak skládání relací jsem pochopila tady na tomto příspěvku: http://forum.matweb.cz/viewtopic.php?id=5287 → velmi dobře vysvětleno!
Ještě jednou velké díky!
Offline
#4 29. 10. 2012 01:17 — Editoval Pavel Brožek (29. 10. 2012 01:18)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Relace: důkaz
↑ kompik:
U těch nekonečných množin, nemyslel jsi spíš  ? Zdá se mi, že pro
? Zdá se mi, že pro  složením relací dostaneme identitu v obou případech.
složením relací dostaneme identitu v obou případech.
Offline
#5 29. 10. 2012 10:59 — Editoval kompik (29. 10. 2012 11:00)
Re: Relace: důkaz
Pavel Brožek napsal(a):
↑ kompik:
U těch nekonečných množin, nemyslel jsi spíš? Zdá se mi, že pro
složením relací dostaneme identitu v obou případech.
Samozrejme, ze je to pravda. Takze druhy pokus, ked vezmem  a relacie
a relacie  a
a  , tak dostaneme:
, tak dostaneme: (pre kazde x mame
(pre kazde x mame  a
a  ; t.j. x->x+1->x.
; t.j. x->x+1->x.
Ale v relacii  nebude dvojica (0,0). (Do nuly sa nemam "ako dostat", nie je ziadne cislo x take, ze
nebude dvojica (0,0). (Do nuly sa nemam "ako dostat", nie je ziadne cislo x take, ze  .)
.)
Dakujem za opravu!
Offline