Matematické Fórum

Kouří se mi v hlavě · 29. 10. 2012 23:09

Ahoj.

Zadání: $a=\{2^{-n}+3^{-n};n\in N\}$ , určete supremum, infimum
1) dosadila jsem za n = 1, získala jsem maximum a to je zároveň i supremum: $sup (A)=\frac{5}{6}$
- důkaz horní závory: $\forall x\in A: x\le sup(A)$
1a) $\frac{1}{2^{n}}+\frac{1}{3^{n}}\le \frac{5}{6}$
1b) $\frac{1}{2^{n}}+\frac{1}{3^{n}}\le \frac{1}{3}+\frac{1}{2}$ → z toho vidíme, že to bude vždy platit

- důkaz nejmenší horní závory:
Nechť $a<\frac{5}{6}$ → n ???
2) $a < \frac{1}{2^{n}}+\frac{1}{3^{n}}<\frac{5}{6}$

Nyní bych měla vyjádřit $n$ je to tak? Pokud bych dokázala, že to platí, tak mám kompletní důkaz?
Další krok by bylo zlogaritmování?

$inf(A)=0$
To nevím, jak dokázat, nevíte někdo?

Pokud by se jednalo o množinu celých čísel, tj. $n\in Z$ , $sup (A)=\emptyset$ a $inf(A)=0$ , jak bych to opět dokázala? Já to pouze „vím“ (intuice), ale nevím, jak to početně vyjádřit...

Díky za jakoukoliv pomoc.

kaja.marik

Supremum nemuze byt prazdna mnozina, kdyztak nekonecno.

to s tim infimem: staci treba dokazat, za nula je i limitou.

ad dukaz nejmensi horni zavory: volite a<5/6. To ale neni horni zavora, protoze je mensi nez prvni clen posloupnosti. Neni tedy co dokazovat.

Kouří se mi v hlavě · 29. 10. 2012 23:27

↑ kaja.marik:

Nekonečno nemáme prý dovolené, mohu říci, že supremum neexistuje ?

Ok, díky .-)

Brano · 30. 10. 2012 11:46

supremum existuje a je to 5/6, sama si zistila, ze 5/6 je maximum a ak maximum existuje, tak existuje aj supremum a je rovne maximu.

pozrime sa na $a < \frac{1}{2^{n}}+\frac{1}{3^{n}}<\frac{5}{6}$
toto vobec ani nieje ziadane, aby platilo.

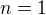ma platit: pre lubovolne $a<5/6$ existuje $n$ take, ze $a < \frac{1}{2^{n}}+\frac{1}{3^{n}}$ , no a pre kazde $a$ zober $n=1$ a mas to.

na to, ze $\inf(A)=0$ si najprv vsimnes, ze $0\le \frac{1}{2^{n}}+\frac{1}{3^{n}}$ .
Teraz potrebujes, ze pre lubovolne $a>0$ existuje $n$ take, ze $\frac{1}{2^{n}}+\frac{1}{3^{n}}<a$ .
Vsimni si, ze $\frac{1}{2^{n}}+\frac{1}{3^{n}}<\frac{1}{2^{n}}+\frac{1}{2^{n}}=\frac{1}{2^{n-1}}$ , dalej to uz zvladnes?

Matematické Fórum

#1 29. 10. 2012 23:09

Supremum, infimum

#2 29. 10. 2012 23:15 — Editoval kaja.marik (29. 10. 2012 23:16)

Re: Supremum, infimum

#3 29. 10. 2012 23:27

Re: Supremum, infimum

#4 30. 10. 2012 11:46

Re: Supremum, infimum

Zápatí