Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3) (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 10. 2012 11:46 — Editoval elektronaut (30. 10. 2012 11:48)
- elektronaut

- Zelenáč
- Příspěvky: 14
- Reputace: 0
inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3)
Dobrý den, potřeboval bych se ujistit ve vzorečku pro výpočet inverzní matice
Pokud mám matici 2x2![kopírovat do textarea $ A =
\left[
\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}
\right]$](/mathtex/4e/4e0d26045ad28512f5f589b0db538b98.gif)
tak inverzi spočítám jako 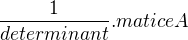
tj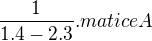
tj![kopírovat do textarea $A^{-1} =
\frac{1}{-2} .
\left[
\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}
\right]
=
\left[
\begin{array}{cc}
-1/2 & -1 \\
-3/2 & -2
\end{array}
\right]$](/mathtex/ff/ff98df2921477d98bc57d701436cb858.gif)
je to spravny postup ?
----------------------------------------------------------
a potom metoda 3x3
je spravny postup
? děkuji moc za odpovědi.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 30. 10. 2012 11:50 — Editoval mikl3 (30. 10. 2012 11:54)
Re: inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3)
↑ elektronaut: inverzní matici vypočítáš jako součin 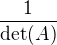 a transponované matice doplňků, neboli adjungované matice, a to platí pro všechny matice regulární
a transponované matice doplňků, neboli adjungované matice, a to platí pro všechny matice regulární
vždy si můžeš provést zkoušku, součin matice původní a inverzní, má vyjít jednotková
Offline
#3 30. 10. 2012 11:57 — Editoval elektronaut (30. 10. 2012 12:00)
- elektronaut

- Zelenáč
- Příspěvky: 14
- Reputace: 0
Re: inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3)
↑ mikl3: děkuji za odpověď, můžu se zeptat jak vypočítám transponovanou matici doplňků (tj adjungovanou matici) pro matici ![kopírovat do textarea $ A =
\left[
\begin{array}{cc}
1 & 2 \\
3 & 4
\end{array}
\right]$](/mathtex/4e/4e0d26045ad28512f5f589b0db538b98.gif)
? děkuji
ps: pro matici 3x3 to spocitam, ale pro 2x2 nevim ?
Offline
#4 30. 10. 2012 12:00 — Editoval vanok (30. 10. 2012 12:26)
Re: inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3)
Ahoj ↑ elektronaut:
Tvoja metoda nie je dobra, mozes to skusit ze vynasobis obe matice... a to ti neda jednotkovu maticu.
Inac, napr vdaka google najdes odpoved na tvoje otazky
Dam ti odpoved na tvoju otazku v pripade matic 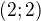
Inverna matica, matice![kopírovat do textarea $ A =
\left[
\begin{array}{cc}
a & b \\
c & d
\end{array}
\right]$](/mathtex/27/27e6f8d4de6383de7c7de1a23177b5a0.gif) ,
,
je ![kopírovat do textarea $ A^{-1}= \frac 1 {\det A} \left[
\begin{array}{cc}
d & -b \\
-c & a
\end{array}
\right]$](/mathtex/6a/6a8903234555955fc55d17ad65422759.gif) ,
,
ak 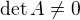
V pripade, ze 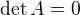 , inverzna matica neexistuje.
, inverzna matica neexistuje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 30. 10. 2012 12:01
- elektronaut

- Zelenáč
- Příspěvky: 14
- Reputace: 0
Re: inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3)
↑ vanok: supr děkuji moc
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » inverzní matice pomocí determinantu (velikost matice 2x2 a 3x3) (TOTO TÉMA JE VYŘEŠENÉ)