Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita řešená rozvojem (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 11. 2012 12:51
Limita řešená rozvojem
Zdravím,
mám za úkol spočítat následující limitu funkce pomocí převedení rozvojem 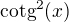
 .
.
Ale nenapadá mě, jak rozvoj funkce 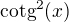 zjistit, protože x jde do nuly, tak potřebuju Maclaurinův rozvoj a
zjistit, protože x jde do nuly, tak potřebuju Maclaurinův rozvoj a 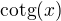 není v nule vůbec definovaná. Kdybych dokázal vyjádřit alespoň
není v nule vůbec definovaná. Kdybych dokázal vyjádřit alespoň 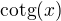 pomocí mocninné řady, tak bych dostal
pomocí mocninné řady, tak bych dostal 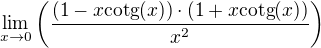
což by mohlo vést k nějakému výsledku. Jakým způsobem se dá spočítat MacLaurinova řada 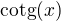 pro
pro  ?
?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#5 03. 11. 2012 14:25 — Editoval vanok (03. 11. 2012 14:25)
Re: Limita řešená rozvojem
Ahoj,
Poznamka: ide skor o pouzitie asymptotickeho rozvoju ( to je generalalizacia ...)
Metoda:
Je uzitocne vediet, ze ze limitovany rozvoj pre 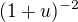 je
je 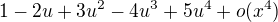
A potom vyjadrit LR pre 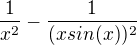 a ukoncit vdaka predoslemu vzorcu.
a ukoncit vdaka predoslemu vzorcu.
Kontrola:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita řešená rozvojem (TOTO TÉMA JE VYŘEŠENÉ)
 ) a pak Taylorovy rozvoje funkcí sinus a cosinus do 2. řádu.
) a pak Taylorovy rozvoje funkcí sinus a cosinus do 2. řádu.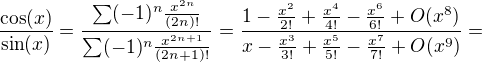
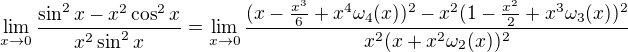
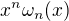 je možné zapsat i pomocí
je možné zapsat i pomocí 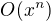 .
.
