Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 06. 11. 2012 22:06

dumpman
Příspěvky: 42
Reputace:   1 
 

Dimenze pruniku linearnich obalu

Ahoj,
potreboval bych se ujistit, jestli postupuji spravne. Mam takovy priklad:

Najdete dimenzi vektoroveho prostoru $P_{1} \cap  P_{2}$ kde $P_{1} = \langle (1, 1, 1, 1), (1,-1, 1,-1), (1, 3, 1, 3) \rangle ; P_{2} = \langle (1, 2, 0, 2), (1, 2, 1, 2), (3, 1, 3, 1) \rangle $

moje reseni:
- spocitam baze 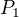$P_{1}$ a $P_{2}$ pomoci gaussovy eliminace a urcim dle hodnosti matice dimenze (3 a 2)
- podobne urcim dimenzi spojeni $P_{1} \vee P_{2}$ (3)
- nyni z vety o dimenzi pruniku a spojeni $dim P_{1} \cap P_{2} = dim P_{1} + dim P_{2} -  dim P_{1} \vee P_{2} = 3+2-3 = 2$

je to OK?

Diky moc za odpoved

\forall n\in \mathbb{N}; \forall x\in \mathbb{\mathbb{R}}; \frac{sinx}{n}= \frac{si\not nx}{\not n}=six=6\ldots qed

Offline

  • (téma jako vyřešené označil(a) dumpman)

#2 06. 11. 2012 23:02

didik
Příspěvky: 109
Reputace:   2 
 

Re: Dimenze pruniku linearnich obalu

Ahoj, postup máš urtiče správný, konečný výsledek mi vyšel také stejně akorát dimenze jednotlivých podprostorů mi vyšli přesně naopak, ale to asi jen překlep.

Vím, že nic nevím.

Offline

 

#3 07. 11. 2012 09:41

dumpman
Příspěvky: 42
Reputace:   1 
 

Re: Dimenze pruniku linearnich obalu

sorry, jasne melo to byt opacne,
diky moc!

\forall n\in \mathbb{N}; \forall x\in \mathbb{\mathbb{R}}; \frac{sinx}{n}= \frac{si\not nx}{\not n}=six=6\ldots qed

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson