Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stá derivace funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 11. 2012 20:19
Stá derivace funkce
Ahoj,
řeším následující úlohu. Chtěl bych spočítat podíl 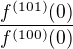 sté plus první a sté derivace v bodě nula funkce
sté plus první a sté derivace v bodě nula funkce 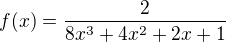 .
.
Uvážil jsem, že bych měl zjistit Taylorův rozvoj v bodě 0 této funkce. Zkusil jsem rozložit na parciální zlomky a dostal jsem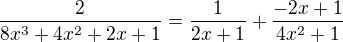
ale nevím, jak pokračovat, jelikož neumím rozložit do řady druhý člen. Poradíte, jak pokračovat?
Děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) Sulfan)
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Stá derivace funkce (TOTO TÉMA JE VYŘEŠENÉ)

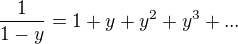
 teraz mozes dosadit
teraz mozes dosadit  a dostanes prvy clen, alebo
a dostanes prvy clen, alebo 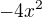 a dostanes menovatel druheho clenu, ktory potom pokojne prenasob citatelom -
a dostanes menovatel druheho clenu, ktory potom pokojne prenasob citatelom - 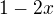 .
.