Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 11. 2012 21:38
Součet nekonečné řady - limita
Dobrý večer,
mohu vás poprosit o pomoc s řešením u příkladu?
Abych udělal součet této řady, tak musím udělat limitu výrazu. Jak ovšem můžu udělat limitu prvního činitele 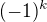 - když osciluje mezi 1 a -1?
- když osciluje mezi 1 a -1?
Offline
- (téma jako vyřešené označil(a) mb305)
#2 09. 11. 2012 21:59
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Součet nekonečné řady - limita
↑ mb305:
Umíme sčítat geometrickou řadu ve tvaru: 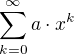 , kde součet je
, kde součet je 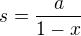 , takže tuto sumu převedeme do požadovaného tvaru. (Samozřejmě
, takže tuto sumu převedeme do požadovaného tvaru. (Samozřejmě
musí platit podmínka, že  ).
).
Zvládneš to dopočítat?
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 09. 11. 2012 22:29
Re: Součet nekonečné řady - limita
↑ Aquabellla:
Supr, po takovéto radě už ano. Děkuji Ti mockrát.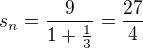
Offline
