Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » zväzy - diskrétna matematika (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 11. 2012 23:58
zväzy - diskrétna matematika
Nech ({1,2,3,4,9,36}, | ) je zväz. Je tento zväz komplementárny, distributívny a booleovský ?
Hasseho diagram pre tento zväz je hexagon a moja odpoveď je, že je komplemetárny, distributívny a teda booleovský.
Kontrola správneho riešenia však hovorí: je komplementárny, nie je distributívny a teda nie je booleovský.
Hexagon však neobsahuje žiadny podzväz, ktorý by bol izomorfný s nedistributívnymi zväzmi typu pentagon alebo diamant.
Robím niekde chybu, že mi vychádza iný výsledok než je očakávaný ?
Ďakujem za radu.
Offline
- (téma jako vyřešené označil(a) etchie)
#2 11. 11. 2012 01:19
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: zväzy - diskrétna matematika
a co napriklad podzvaz {1,2,3,4,36} alebo {1,2,4,9,36}, v podstate mozes vynechat ktorykolvek z prvkov 2,3,4,9 a ziskas pentagon.
Offline
#3 11. 11. 2012 10:29
Re: zväzy - diskrétna matematika
↑ JohnPeca18:
hm, tak potom ja pod pojmom podzväz chápem asi niečo iné, než to v skutočnosti je.
vychádzam z definície zväzu z prednášok a zo skrípt, ale nikde tam vlastne nie je povedané, čo to podzväz je.
čo presne teda je podzväz ?
Offline
#4 11. 11. 2012 11:20
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: zväzy - diskrétna matematika
Hm, z toho co som nasiel je podzvaz podmnozina prvkov zvazu, so stejnou operaci usporadani a uzavrena na suprema a infima.
Offline
#6 11. 11. 2012 16:28
Re: zväzy - diskrétna matematika
↑ kompik:
áno, toto mi je jasné. rád by som však vedel ako nejako praktickejšie overovať distributívnosť zväzov.
to akože treba pre každú trojicu prvkov vo zväze overovať, či platí distributívny zákon ?
však v takom zväze 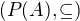 kde A={a,b,c,d} a P(A) je potenčná množina množiny A
kde A={a,b,c,d} a P(A) je potenčná množina množiny A
mi iba vykreslenie Hasseho diagramu pre hyperkocku trvalo takú hodinu (aspoň som si dokázal nakresliť "nepredstaviteľný" útvar). Ale čo už si vôbec neviem predstaviť je, že by som mal ešte overovať pomocou distributívneho zákona, že či je tento zväz distributívny. Viem že je distributívny, ale to preto, že som to čítal. Ale nemusí ísť ani o hyperkocku, stačí trošku zložitejší zväz a už sa to zamotáva. Grafické určovanie sa mi zdá lepšie, ale tam som zas ja niečo nepochopil, preto pátram po vysvetlení pojmu podzväz, a teda čo (aké grafické úkony so zväzom) môžem a nemôžem robiť keď chcem zistiť, či je podzväz izomorfný s diamantom alebo pentagonom.
Offline
#7 11. 11. 2012 16:56
Re: zväzy - diskrétna matematika
etchie napsal(a):
áno, toto mi je jasné. rád by som však vedel ako nejako praktickejšie overovať distributívnosť zväzov.
to akože treba pre každú trojicu prvkov vo zväze overovať, či platí distributívny zákon ?
Toto je asi najjednoduchsie riesenie (v zmysle riesenie hrubou silou - netreba tam ziadnu myslienku). A pokial by bol zvaz zadany diagramom, t.j. nevies, ako operacie na nom vznikli, tak na prvy pohlad nevidim nejake signifikatne odlisne riesenie.
Ak vsak clovek pozrie na obrazok, tak niekedy lahko zbada, ci tam je ako podzvaz pentagon alebo diamant. Ked vies zdovodnit nedistributivnost v nich, tak pouzijes to iste. (Co je presne to, co som spravil tu.) Samozrejme, taketo riesenie sa zle algoritmizuje - je tazko povedat pocitacu "pozri sa na obrazok a zbadas tam nejaky pozvaz".
etchie napsal(a):
však v takom zväze
kde A={a,b,c,d} a P(A) je potenčná množina množiny A
mi iba vykreslenie Hasseho diagramu pre hyperkocku trvalo takú hodinu (aspoň som si dokázal nakresliť "nepredstaviteľný" útvar). Ale čo už si vôbec neviem predstaviť je, že by som mal ešte overovať pomocou distributívneho zákona, že či je tento zväz distributívny. Viem že je distributívny, ale to preto, že som to čítal. Ale nemusí ísť ani o hyperkocku, stačí trošku zložitejší zväz a už sa to zamotáva. Grafické určovanie sa mi zdá lepšie, ale tam som zas ja niečo nepochopil, preto pátram po vysvetlení pojmu podzväz, a teda čo (aké grafické úkony so zväzom) môžem a nemôžem robiť keď chcem zistiť, či je podzväz izomorfný s diamantom alebo pentagonom.
Tak pre hyperkocku by si to urcite neoveroval pre vsetky trojice, pretoze tam vies ako vyzera spojenie a priesek, a viez z pre mozniny plati 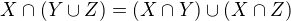 .
.
preto pátram po vysvetlení pojmu podzväz
je to tak ako pisal kolega - vid aj link na Wiki, co som dal
(aspoň som si dokázal nakresliť "nepredstaviteľný" útvar)
Hej vzniknu tam pekne obrazky. Tu je to v casti o Hasseho diagramoch nakreslene pre 2-,3-,4- a 5-prvkovu mnozinu.
Asi nic velmi inteligentne neviem povedat v takejto vseobecnosti, ked sa pytas "ako to budem riesit, ked dostanem iny zvaz".
Offline
#8 13. 11. 2012 20:34
Re: zväzy - diskrétna matematika
↑ kompik:
predsa mi len stále nedá táto vec s tým podzväzom.
mám takýto príklad
a si myslím , že odpoveď c) by mala byť áno
lebo zväz z bodu c) je práve spomínaná 5-rozmerná hyperkocka a zväz 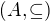 je rovnaký ako podzväz s prvkami vyznačenými červenou farbou. tj. je jeho podzväzom
je rovnaký ako podzväz s prvkami vyznačenými červenou farbou. tj. je jeho podzväzom
je chyba vo výsledku riešenia alebo tomu ešte stále nerozumiem ?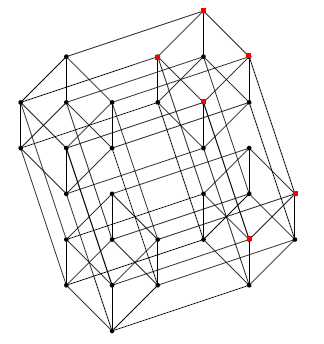
Offline
#9 13. 11. 2012 20:41 — Editoval kompik (13. 11. 2012 20:45)
Re: zväzy - diskrétna matematika
↑ etchie:
Podzvaz by mal zodpovedat podmnozine zvazu uzavretej na prieseky a spojenia. (Prieseky a spojenia su z povodneho zvazu. Nova struktura mozno moze byt zvaz s inymi operaciami.)
V tomto pripade 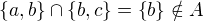 .
.
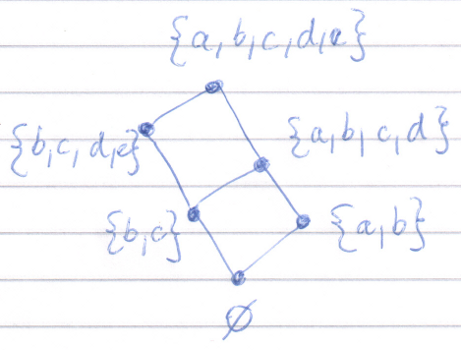
A ten obrazok sa mi nezda, lebo prazdna mnozina by mala byt nakreslena uplne dole.
EDIT:
Este som sa chcel spytat, ze ake su to skripta. (Ak su na webe, tak link potesi.)
Priznam sa, ze zatial nevidim jednoduchy sposob ako overit tu distributivnost.
Offline
#12 13. 11. 2012 22:11
Re: zväzy - diskrétna matematika
↑ kompik:
ďakujem za trpezlivosť pri vysvetľovaní.
myslím, že už som sa posunul o niečo ďalej (nechcem predčasne tvrdiť, že tomu rozumiem na 100%)
stále som sa na to pozeral iba z pohľadu grafiky a hodnoty operácií mi nič nehovorili.
ale vlastne na to, aby som zistil či zväz z príkladu 2.30 je podvzäzom 5-rozmernej hyperkocky, tak nepotrebujem vidieť celú hyperkocku, ale len jej začiatok tj. body {}, {a}, {b},{c},{d},{e},{a,b},{b,c}
a z týchto bodov vidím, že je nemožné aby operácie (v tomto prípade priesek) boli rovnaké
a druhá vec, že ten zväz by kľudne MOHOL byť podzväzom 5-rozmernej hyperkocky, tj. graficky by sa nič nemenilo, ale diagram hyperkocky by bol vystavaný nie z P(X) a relácie "je podmnožinou", ale z iných prvkov prípadne aj z inej relácie, a to práve z takých kde by platili všetky operácie z pôvodného zväzu
Offline
#13 14. 11. 2012 17:55
Re: zväzy - diskrétna matematika
etchie napsal(a):
a druhá vec, že ten zväz by kľudne MOHOL byť podzväzom 5-rozmernej hyperkocky, tj. graficky by sa nič nemenilo, ale diagram hyperkocky by bol vystavaný nie z P(X) a relácie "je podmnožinou", ale z iných prvkov prípadne aj z inej relácie, a to práve z takých kde by platili všetky operácie z pôvodného zväzu
No vidis, toto som si ja vobec neuvedomil.
Porovnanim s Tvojim obrazkom vidno, ze je to izomorfne so zvazom pozostavajucim z mnozin
{}, {a}, {b}, {a,b}, {a,b,c}, {b,c}
(pri usporiadani inkluziou).
Toto je uz naozaj podzvaz P(X), a teda musi byt distributivny.
Takze aj ten povodny zvaz je distributivny, kedze je izomorfny (ma rovnaky Hasseho diagram).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » zväzy - diskrétna matematika (TOTO TÉMA JE VYŘEŠENÉ)
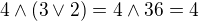
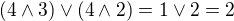
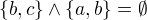 .)
.)