Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 11. 2012 23:19
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Suma
Ahoj,
mým úkolem je zjistit, která čísla se skrývají za těmito sumami:
Nechala jsem je vygenerovat pomocí WA a vidím v nich Fibonacciho posloupnost.
Jak by se ovšem daly ty sumy zjednodušit, aby to bylo vidět na první pohled?
Díky za pomoc.
Offline
- (téma jako vyřešené označil(a) Kouří se mi v hlavě)
#3 06. 11. 2012 10:34
- Kouří se mi v hlavě
- Příspěvky: 82
- Reputace: 1
Re: Suma
↑ Brano:
Bohužel nevím jak, mohl bys prosím připojit i komentář operací?
(Nevím, jak upravovat kombinační čísla, mea culpa, na to stačí držet se základních vlastností, co uvádí Wiki?) Moje mezery jsou v kombinatorice opravdu obrovské, sorry za ně, snažím se to co nejrychleji napravit..
Offline
#4 06. 11. 2012 12:31 — Editoval Brano (06. 11. 2012 12:33)
Re: Suma
Prvy vztah: prvy clen sumy (pre 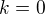 ) vlavo
) vlavo  a ostatne su potom v sume
a ostatne su potom v sume  urob substituciu
urob substituciu  a mas tu sumu vpravo ak premenujes naspat
a mas tu sumu vpravo ak premenujes naspat 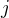 na
na  .
.
Druhy vztah: tu som len vybral posledny clen  .
.
Treti vztah: http://cs.wikipedia.org/wiki/Kombina%C4 … D%C3%ADslo
zakladna vlastnost - piata zhora - mozes si lahko dokazat z faktorialoveho vyjadrenia.
Stvrty vztah: tam je vybraty prvy aj posledny clen, ktore su znova 1 a substitucia v indexe  a znova premenovat naspat na
a znova premenovat naspat na  .
.
Teraz ked scitas prvu a druhu rovnost a vpravo pouzijes treti vztah, tak ti vyjde, ze "prva suma s n"+"druha suma s n" = "prva suma s (n+1)" (z toho ako je rozpisana v stvrtom vztahu).
Este potrebujes dokazat "druha suma s n" + "prva suma s (n+1)" = "druha suma s (n+1)"
a potom mas ukazane, ze je to naozaj Fibonacciho postupnost. To druhe je lahsie - vyskusaj si to sam, aby si si overil, ze si to pochopil.
Offline
#5 13. 11. 2012 01:17
#6 13. 11. 2012 12:43
Re: Suma


Chces dokazat, ze  je Fibonacciho postupnost, cize musis ukazat, ze
je Fibonacciho postupnost, cize musis ukazat, ze  a
a  a ze
a ze  . To posledne je lahke.
. To posledne je lahke.
Ja som ti ukazoval ako sa zvladne 
 a
a 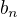 si upravis tak ako som napisal
si upravis tak ako som napisal
![kopírovat do textarea $2+\sum_0^{n-1}\left[{n+k+1 \choose n-k}+{n+k+1 \choose n-k-1}\right]=2+\sum_0^{n-1}{n+k+2 \choose n-k}=\sum_0^{n+1}{n+1+k \choose n+1-k}=a_{n+1}$](/mathtex/32/32195b94217cff9849eb3d5524d5ebc4.gif)
A ak to spravne chapem, tak nerozumies odkial sa vzala predposledna rovnost, tak tu je rozpisana.
a teraz 
![kopírovat do textarea $b_n+a_{n+1}=\sum_0^n{n+k+1 \choose n-k}+\sum_0^{n+1}{n+1+k \choose n+1-k}=\sum_0^n\left[{n+k+1 \choose n-k}+{n+1+k \choose n+1-k}\right]+{2n+2 \choose 0}=$](/mathtex/e5/e506f6bcda67c939142ac89c9a88cd4d.gif)

Offline




