Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica kolmej projekcie (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 11. 2012 17:08
Matica kolmej projekcie
Ahoj, mám príklad:
"Napište matici zobrazení kolmé projekce do roviny procházející počátkem a kolmé na vektor 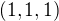 "
"
Nejaký hint? :)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#2 17. 11. 2012 18:44
Re: Matica kolmej projekcie
Ahoj ↑ hradecek:,
Teoria je jednoducha
Nech mame jeden unitarny vektor normalny na rovinu, potom ortogonalna projekcia sa pise
A pochopitelne ak pozname suradnice vektoru v, je lahke najt tvoju maticu.
POZOR, normalny vektor je kolny na rovinu a ma normu ( dlzku 1) ....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 17. 11. 2012 21:01
Re: Matica kolmej projekcie
↑ vanok:
No nie som si istý, či ťa úplne chápem...
Takže normálový vektor je  a môj vektor
a môj vektor 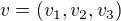 ale ako vytlčiem z tohoto maticu?
ale ako vytlčiem z tohoto maticu?
A odkial si zobral ten vzorec?
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 17. 11. 2012 23:07
Re: Matica kolmej projekcie
↑ hradecek:,
Poznamka : 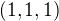 nie je normalizovany, vsak nema normu 1,ale....som isty ze to dokazes opravit.
nie je normalizovany, vsak nema normu 1,ale....som isty ze to dokazes opravit.
Relacia co som napisal, jednoducho vyjadruje, ze P(x) je projekcia : je v rovine, lebo
P(x) je kolmy z v ( skalarny sucet ti to potvrdi),
a x je sucet P(x) a jedneho kolmeho vektoru na rovinu.
( nemas skripta? Daj ich sem online, aby som mohol overit, co ste videli)
Unitarny vektor v je potrebny vo vypoctoch.
Maticu v standardej base najdes jednoducho, ze urcis obrazy vektorov tento bazy.
(poznamka: suradnice pocitaneho vektoru su v standardnej baze, ako aj vypocitany vektor je vyjadreny v tej istej baze )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 18. 11. 2012 01:18
Re: Matica kolmej projekcie
Napadá mě ještě jeden postup vhodný pokud si nepamatuješ nebo hned nevíš vzorec pro OG projekci.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matica kolmej projekcie (TOTO TÉMA JE VYŘEŠENÉ)

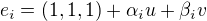 ,
, 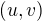 je libovolná báze roviny. V matici budou zapsány po sloupcích vektory:
je libovolná báze roviny. V matici budou zapsány po sloupcích vektory: 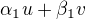 ,
, 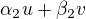 ,
, 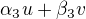 . Tento postup je určitě pomalejší, protože musíš řešit soustavy rovnic pro výsledné vektory. Uvádím ho protože mi přijde názorný.
. Tento postup je určitě pomalejší, protože musíš řešit soustavy rovnic pro výsledné vektory. Uvádím ho protože mi přijde názorný.