Matematické Fórum

JohnPeca18

↑↑ jarry:
No spor to neni, protoze pokud a<b tak plati ze i 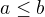$a\leq b$ . Nas profesor na analyze nam rikal, ze tento prosty fakt studenti prehlizeji jako krajinu v pozadi. Ale prinejmensim je to ode mne zbabele a matouci, klidne tam muzes dat ostrou nerovnost.
$(1+\frac{1}{n})^n< e \leq (1+\frac{1}{n})^{n+1}$
taky
$1+x=e^x$
jenom pro x=0. Co teda v pripade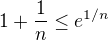
$1+\frac{1}{n}\leq e^{1/n}$
nenastane. A nastane to prave jenom limitne.

Matematické Fórum

#51 21. 11. 2012 09:21 — Editoval JohnPeca18 (21. 11. 2012 09:23)

Re: limita posloupnosti

Zápatí