Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 11. 2012 19:24
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Spojitost
Zdravím, je to asi tou angínou, co mám, ale zarazil jsem se nad tím, jestli je na intervalu  funkce
funkce  spojitá.
spojitá.
Respektive myslel jsem si, že aby byla funkce spojitá, musí mít vlastní limitu (zprava nebo zleva, když v tom bodě není definovaná). Tady je limita  Nebo je má teorie špatná?
Nebo je má teorie špatná?
Asi mám blackout, předem dík za odpověď.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 25. 11. 2012 20:01 — Editoval Jan Jícha (25. 11. 2012 20:02)
#4 25. 11. 2012 22:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Jan Jícha:
Na intervalu (0, 1) je spojitá, na tomto intervalu není žádný bod nespojitosti, lze vyčíslit limity v 0 zprava a v 1 zleva. Na grafu bude mít jen prázdná kolečka na koncích intervalu. Předchozí interval s 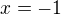 je spíš zajímavý, zda je nespojitost odstranitelná nebo ne (tedy druh bodu nespojitosti).
je spíš zajímavý, zda je nespojitost odstranitelná nebo ne (tedy druh bodu nespojitosti).
Jinak vždy práci s funkci je třeba začínat vyšetřením def. oboru, jen připomenu :-)
Offline
#5 25. 11. 2012 22:11
#6 25. 11. 2012 22:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Jan Jícha:
Chce to mít knihu :-)
Měj se.
Offline
#7 26. 11. 2012 08:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Jan Jícha:
Ještě téma otevřu, pro jistotu přidej, prosím, svou definici. Děkuji.
Offline
#8 26. 11. 2012 11:01
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Spojitost
No já měl napsáno, že aby byla funkce spojitá na intervalu 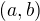 , musí být spojitá v každém bodě
, musí být spojitá v každém bodě  a v těchto bodech
a v těchto bodech  a
a  musí mít vlastní limitu (a pokud není v tomto bodě definovaná, musí mít vlastní limitu zprava nebo zleva).
musí mít vlastní limitu (a pokud není v tomto bodě definovaná, musí mít vlastní limitu zprava nebo zleva).
Offline
#9 26. 11. 2012 11:10 — Editoval ((:-)) (26. 11. 2012 11:11)
Re: Spojitost
Offline
#10 26. 11. 2012 11:30 — Editoval Rumburak (26. 11. 2012 11:33)
Re: Spojitost
↑ Jan Jícha:
Zdravím. Ovbyklá defnice spjitosti funkce na množině je:
"Funkce f je spojitá na množině M, právě když je spojitá vzhledem k množině M v každém jejím bodě."
Pokud M je otevřená množina, pak můžeme specifikaci "vzhledem k množině M" vynechat.
Offline
#11 26. 11. 2012 11:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Jan Jícha:
Děkuji, řekla bych, že to souhlasí, jak si to představuji. Ovšem chybí tomu podmínka, že vyšetřovaný bod musí patřit do def. oboru funkce Opraveno: "Chybělo tomu zjištění, zda vyšetřovaný bod patří do def. oboru funkce" - tak?
Tedy pokud se vrátím k původnímu intervalu  rozkladem jmenovatele na součin se zjistilo 2 body, pro které je jmenovatel nulový. Jeden
rozkladem jmenovatele na součin se zjistilo 2 body, pro které je jmenovatel nulový. Jeden 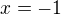 byl vnitřním bodem intervalu (a je bodem nespojitosti, jelikož do def. oboru nepatří) a na obrázku musí být prázdné kolečko.
byl vnitřním bodem intervalu (a je bodem nespojitosti, jelikož do def. oboru nepatří) a na obrázku musí být prázdné kolečko.
Za podmínky, že x není (-1), potom můžeme předpis funkce upravit po vykrácení.
Při vyšetření okrajů intervalu  v bodě
v bodě  je nespojitost z důvodu, jak jsi napsal
je nespojitost z důvodu, jak jsi napsal  . V bodě (-2) je vlastní limita, tedy je stejný závěr ↑ jelena:.
. V bodě (-2) je vlastní limita, tedy je stejný závěr ↑ jelena:.
A to už by snad mělo být komplet a teď počkám na spravedlivou kritiku. Děkuji.
Offline
#12 26. 11. 2012 11:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Rumburak:
děkuji, ještě prosím spravedlivou kritiku. Zdravím.
Offline
#14 26. 11. 2012 12:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Rumburak:
určitě to nehoří. I více mých příspěvků v tomto tématu. V příspěvku 11 jsem kurzivou opravila 2. větu, ta se vztahuje ještě k úvodnímu příspěvku, ne k definici od kolegy Honzy.
Offline
#15 26. 11. 2012 17:04 — Editoval Rumburak (27. 11. 2012 17:10)
Re: Spojitost
Definice uvedená v ↑ Rumburak: se používá v obecné topologii. Podle ní by platilo v souladu s obecnými představami například
(1) funkce tg je spojitá na množině  ,
,
(2) funkce arcsin je spojitá na intervalu  ,
,
ale také
(3) funkce sgn je spojitá na množině {0} , neboť odmyslíme-li si všechny nenulové body reálné osy (což je součást obsahu pojmu
ralativní spojitosti vzhledem k množině 0), nezbude tam žádný, který by spojitost (vzhledem k množině {0}) v bodě 0 porušil.
V kursech elementární analýzy funkcí jedné proměnné se o množině M z definice v ↑ Rumburak: zpravidla ještě přadpokládá,
že je intervalem kladné délky nebo sjednocení (konečně mnoha nebo spočetně mnoha) takových intervalů.
Další poznámky:
Pro kolegu Jana Jíchu :
Spojitost funkce f v bodě x znamená, že existuje v tomto bodě limita (odpovídající zvolenému pojetí spojitosti), která zároveň JE ROVNA
HODNOTĚ f(x) - viz definice spojitosti v bodě. Jde tedy o víc, než že existuje příslušná (vlastní) limita . Pokud by tedy f(x) nebylo definováno,
pak hovořit o spojitosti funkce f v bodě x by nemělo by smysl.
Krajní body otevřeného intervalu (-2, 2) do něj nepatří, takže řešíme-li spojitost funkce f na tomto intervalu, pak se o body -2, +2 nemusíme starat.
Pro kolegyni Jelenu :
V bodě (-2) je vlastní limita, tedy je stejný závěr
toto jsem úplně nepochpoil, ale ještě se nad tím zamyslím :-).
Offline
#16 26. 11. 2012 20:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Rumburak:
:-)
toto jsem úplně nepochopil, ale ještě se nad tím zamyslím :-).
není nad čím :-) V tématu názorně ukazuji syndrom stonožky. V ↑ 2. příspěvku: jasně reaguji, že je třeba vyšetřit def. obor a najít jiný bod nespojitosti, než okrajové body intervalu.
A potom jsem učinila pokus přemýšlet :-) Následky jsou zřejmé.
Děkuji velice za výklad.
Offline
#17 27. 11. 2012 15:06
#18 27. 11. 2012 22:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spojitost
↑ Jan Jícha:
děkuji za sdělení a za pozdrav :-) Označím za vyřešené (i když nevím, zda podle představy uživatele téma Moderátora by neměl označovat osobně Administrátor :-)
V manuálu o tom nic není.
Offline
