Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 11. 2012 11:29
definícia zväzu
Def: Zväz je čiastočne usporiadaná množina, v ktorej každé 2 prvky majú spojenie a priesek.
Je ekvivalentným aj tvrdenie, že zväz je ČUM, kde existuje najmenší a najväčší prvok ?
Najmenší a najväčší prvok môže byť vždy iba jeden, čiže je porovnateľný so všetkými ostatnými, a to by malo zabezpečiť, že každé 2 prvky budú mať spojenie aj priesek. Je to tak ?
(Definícia zväzu sa mi v hlave vždy vybaví tým druhým spôsobom, ale neviem či to je ok).
Ďakujem
Offline
- (téma jako vyřešené označil(a) etchie)
#2 28. 11. 2012 16:05
Re: definícia zväzu
etchie napsal(a):
Def: Zväz je čiastočne usporiadaná množina, v ktorej každé 2 prvky majú spojenie a priesek.
Je ekvivalentným aj tvrdenie, že zväz je ČUM, kde existuje najmenší a najväčší prvok ?
Nie. Prvý kontrapríklad, ktorý mi prišiel na um, je takýto:
Pridáme k intervalu ![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) ešte jeden nový prvok, ktorý bude "rovnako vysoko" ako 0, t.j. naša množina bude
ešte jeden nový prvok, ktorý bude "rovnako vysoko" ako 0, t.j. naša množina bude ![kopírovat do textarea $[-1,1]\cup\{0'\}$](/mathtex/da/da373968c6ffc1a27c4d94f7af4391a9.gif)
 pre
pre ![kopírovat do textarea $a,b\in[-1,1]$](/mathtex/df/df1efb4f9f10983586c88416b566de46.gif) (prvky z
(prvky z ![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) sú usporiadané obvykle)
sú usporiadané obvykle) pre
pre ![kopírovat do textarea $b\in[-1,1]$](/mathtex/f7/f7d3ece258059617d772d522504c69ba.gif)
 pre
pre ![kopírovat do textarea $a\in[-1,1]$](/mathtex/b7/b782a4fe31eeb694191081d6bb6df10a.gif) (od
(od  sú väčšie tie isté prvky ako od nuly)
sú väčšie tie isté prvky ako od nuly)
Táto čiastočne usporiadaná množina má najväčší aj najmenší prvok, ale neexistuje  ani
ani  .
.
Offline
#3 28. 11. 2012 17:46
Re: definícia zväzu
↑ kompik:
fíha, to sú mi veci... klobúk dolu, že si dokážeš takéto abstrakcie zhmotniť.
len aby som si bol istý, či ten kontrapríklad chápem správne:![kopírovat do textarea $[-1,1]$](/mathtex/f5/f5d766fbe82b7d375db132c40fdc0732.gif) je to isté ako interval
je to isté ako interval 
čo by som si mohol v kvázi Hasseho diagrame predstaviť ako reťazec začínajúci od -1, smerujúci hore, v mieste kde by mala byť 0 sa reťazec "rozdvojí" na 0 a 0' a potom "spojí" a pokračuje smerom k 1. pričom ale je to len taká nedokonalá pomôcka lebo sa tam nič spojiť ani rozdvojiť nemôže - lebo práve tie 2 body by tvorili priesek a spojenie, ktoré neexistujú.
finta je v tom, že interval pracuje s reálnymi číslami a v mojej pomôcke sa tvárim, že čísla sú zo Z (čo nie sú).
takže to môžem uzavrieť tak, že moja úvaha o ekvivalentnej definícii zväzu sa vôbec nezaoberala možnosťou zväzov na množine R, a preto som došiel k nesprávnemu záveru ? pre úvahy v nespojitých množinách ako N a Z, by to ale ekvivalentné tvrdenie asi bolo.
a je to taký zaujímavý paradox. diskrétna matematika (tj. nespojitá) dokáže pracovať aj so spojitými štruktúrami.
Hasseho diagram sa však pre tieto spojité štruktúry nakresliť nedá - lebo majú nekonečne veľa bodov - ale predstaviť sa dá.
Offline
#4 28. 11. 2012 17:56
Re: definícia zväzu
etchie napsal(a):
↑ kompik:
takže to môžem uzavrieť tak, že moja úvaha o ekvivalentnej definícii zväzu sa vôbec nezaoberala možnosťou zväzov na množine R, a preto som došiel k nesprávnemu záveru ? pre úvahy v nespojitých množinách ako N a Z, by to ale ekvivalentné tvrdenie asi bolo.
Nie je celkom jasné, čo myslíš pod spojitými a nespojitými množinami; ale ten kontrapríklad sa dá spraviť aj pre spočítateľnú množinu, jednoducho nahraď [-1,1] množinou  .
.
Túto množinu vieš vcelku jednoducho bijekciou zobraziť na Z, čiže dalo by sa nájsť také usporiadanie na množine Z. (Ale jednoduchšie je ho popísať cez tamtú množinu, keďže na nej berieme obvyklé usporiadanie.0
Offline
#5 28. 11. 2012 18:15
Re: definícia zväzu
↑ kompik:
ok, ďakujem. ten môj popis toho, čo si predstavujem, nie je presný.
mal som na mysli konečné množiny - lebo s tými mozog bežne pracuje bez problémov.
takže môžem to tvrdenie uzavrieť na konečné množiny ? N, Z ani R také nie sú.
Offline
#6 28. 11. 2012 18:38
Re: definícia zväzu
↑ etchie:
A teda všetko som to úplne zbytočne komplikoval.
Hneď ako prvé som mal povedať, že zväz nemusí mať najväčší/najmenší prvok. Čiže jednoduchší kontrapríklad pre nekonečné množiny by bol Z s obvyklým usporiadaním.
Pre konečné množiny to fungovať bude - akonáhle tam máme horné ohraničenie pre nejakú množinu, tak bude existovať aj najmenšie horné ohraničenie; inak by tam musel byť nekonečný klesajúci reťazec.
Offline
#7 28. 11. 2012 18:49
Re: definícia zväzu
A teda všetko som to úplne zbytočne komplikoval.
určite nie, inak by som sa k týmto informáciám buď neprepracoval vôbec alebo vo veľmi dlhom čase.
riešil som príklady na zväzy - všetko konečné množiny - a z toho som nadobudol mentálny syndróm "thinking in the box".
a vďaka tvojim kontrapríkladom vidím, že tu je aj svet "out of the box", ktorý som prehliadal.
takže vďaka za skvelé vysvetlenie.
Offline
#9 29. 11. 2012 18:04
Re: definícia zväzu
↑ Andrejka3:
áno to je pravda,
týmto je "alternatívne" tvrdenie komplet vyvrátené. Už z neho nič nezostalo.
takže: Zväz je na večné časy čiastočne usporiadaná množina, v ktorej každé 2 prvky majú spojenie a priesek. A nikdy inak...
Radšej si to tu pekne napíšem, aby sa mi vrylo do pamäti práve toto tvrdenie.
Offline

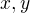 nemá infimum.
nemá infimum.