Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kvadratická (non)residua (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 11. 2012 00:37
Kvadratická (non)residua
Ahoj,
zítra píšu test a do teď jsem si myslel, že kvadratická (non)residua chápu, ale asi jsem se v tom nějak zamotal.
Najděte kvadratická residua modulu m=7
Vždy to dělám tak, že si udělám tabulku se sloupci  ,
,  a
a 
x  a
a
1 1 1
2 4 4
3 9 2
4 16 2
5 25 4
6 36 1
Pro kvadratická residua by mělo platit, že gcd(a, m) = 1 a 
Pro kvadratická non-residua by mělo platit, že gcd(a, m) = 1
Tudíž by pak kvadratická residua byly  , ale správný výsledek je residua = {1,2.4} a nonresidua = (3,5,6)
, ale správný výsledek je residua = {1,2.4} a nonresidua = (3,5,6)
Co dělám špatně?
Díky moc!
Navštivte portál Matematika pro každého! http://maths.cz
Offline
- (téma jako vyřešené označil(a) Blujacker)
#2 30. 11. 2012 02:57 — Editoval vanok (30. 11. 2012 03:09)
Re: Kvadratická (non)residua
Ahoj,
Kvadraticke résidus su rozne mozne nenulove hodnoty a v tvojej tatulke
Ako mozes vidiet su to 1, 2, 4. ( tak mod 7 su tri)
Vseobecne mod p, ( prvocislo) mas ich 
Na skuske by som sa ta spytal kedy -1 je kvadraticke residus.....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 30. 11. 2012 09:23
Re: Kvadratická (non)residua
↑ vanok:
Omlouvám se, ale asi nerozumím. Jak se tedy pozná rozdíl mezi residuem a nonresiduem? Ty omezující podmínky, co jsem napsal jsou dobře? Když to tedy vezmu postupně pro každé číslo z tabulky, tak:
1) gcd(1, 7) = 1 a současně platí  -> číslo 1 je kvadratické residuum modulu 7.
-> číslo 1 je kvadratické residuum modulu 7.
3) gcd(4, 7) = 1 a současně platí  -> číslo 2 je kvadratické residuum modulu 7.
-> číslo 2 je kvadratické residuum modulu 7.
3) gcd(2, 7) = 1 a současně platí  -> číslo 3 je kvadratické residuum modulu 7.
-> číslo 3 je kvadratické residuum modulu 7.
4) gcd(2, 7) = 1 a současně platí  -> číslo 4 je kvadratické residuum modulu 7.
-> číslo 4 je kvadratické residuum modulu 7.
5) gcd(4, 7) = 1 a současně platí  -> číslo 5 je kvadratické residuum modulu 7.
-> číslo 5 je kvadratické residuum modulu 7.
6) gcd(1, 7) = 1 a současně platí  -> číslo 6 je kvadratické residuum modulu 7.
-> číslo 6 je kvadratické residuum modulu 7.
Ale, jak jste Vy sám řekl, správná residua jsou pouze {1, 2, 4}. Jakto?
Děkuji
Navštivte portál Matematika pro každého! http://maths.cz
Offline
#4 30. 11. 2012 09:42
Re: Kvadratická (non)residua
Co pises mas trochu pomylene.
Ako je definovane residus?
Je to prvok ktory je stvorec nejakeho ineho nenuloveho prvku.
Co pises vyssie nema nic spolocne z definiciou. Lebo si to obratil na opak (a mimochodom kazde cislo mensie ako nejake prvocislo je z nim nesudelitelne.... )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 30. 11. 2012 10:01 — Editoval Blujacker (30. 11. 2012 10:27)
Re: Kvadratická (non)residua
↑ vanok:
Už jsem to možná pochopil. Zkusím zde určit kvadratická residua a nonresidua pro modul m = 10 a Vás prosím, abyste mi řekl, zda můj postup už je správný.
x  a
a
1 1 1 residuum
2 4 4 gcd(10, 4) != 1
3 9 9 residuum
4 16 6 gcd(10, 6) != 1
5 25 5 gcd(10, 5) != 1
6 36 6 gcd(10, 6) != 1
7 49 9 residuum
8 64 4 gcd(10, 4 != 1
9 81 1 residuum
Residua = {1, 9}
Non-residua = {3, 7, 9}
Děkuji za Váš čas
EDIT: Kvadratické residuo máme zadané takto: Nechť m je kladné celé číslo. Číslo a je kvadratické residuum modulo m, když gcd(a, m) = 1 a kongruence  má nějaké řešení. Když tato kongruence nemá žádné řešení a je kvadratické non-residuum modulo m.
má nějaké řešení. Když tato kongruence nemá žádné řešení a je kvadratické non-residuum modulo m.
Navštivte portál Matematika pro každého! http://maths.cz
Offline
#6 30. 11. 2012 13:04
Re: Kvadratická (non)residua
Teraz si presne pouzil definiciu.
A ako si videl ak pracujes z p prvocislo, je to este jednoduchsie.
Dobre pokracovanie a uspech na skuske.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 30. 11. 2012 18:21
Re: Kvadratická (non)residua
Děkuji, štěstí na zkoušce bylo poloviční. Byla tam otázka: [i]Určtete, zda je 2 kvadratickým residuem čísla 7, a když ano, určete všechny jeho odmonicny. [i].
Úspěšně jsem určil, že to residuum je, ale o odmocninách jsem slyšel prvně :-) Snad bude dostatek bodů z dalších příkladů.
Navštivte portál Matematika pro každého! http://maths.cz
Offline
#8 30. 11. 2012 18:34
Re: Kvadratická (non)residua
↑ Blujacker:,
Vsak odpoved mas v tej tabulke co si napisal na zaciatku .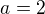 pre x=3 alebo 4.
pre x=3 alebo 4.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 30. 11. 2012 18:58
Re: Kvadratická (non)residua
↑ vanok:
Škoda, tohle vědět dříve :-) Ale i tak děkuji!
Navštivte portál Matematika pro každého! http://maths.cz
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kvadratická (non)residua (TOTO TÉMA JE VYŘEŠENÉ)
