Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 02. 12. 2012 20:36 — Editoval BakyX (02. 12. 2012 20:37)
Re: Derivace a Optika
Ahoj.
Krok číslo 1, nakresliť si obrázok. To by nemal byť problém.
V druhom kroku je treba vyjadriť uhol, ktorý maximalizuješ pomocou konštánt a neznámej vzdialenosti pozorovateľa od steny, ktorú môžme označiť  .
.
Používam označenie: označuje "stred" oka pozorovateľa.
označuje "stred" oka pozorovateľa.  označuje spodný okraj obrazu.
označuje spodný okraj obrazu.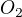 označuje horný okraj obrazu.
označuje horný okraj obrazu. označuje päta kolmice z
označuje päta kolmice z  na
na 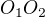 (tj.
(tj. 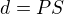 )
)
Zorný uhol je  . Potrebujeme vyjadriť napríklad jeho sínus. To môžme nasledovne:
. Potrebujeme vyjadriť napríklad jeho sínus. To môžme nasledovne:
1. Zo sínusovej vety pre 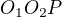 ho vyjadríme cez
ho vyjadríme cez 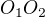 ,
, 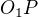 a
a 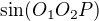 .
.
2. 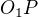 vyjadríme ako preponu v pravouhlom trojuholníku.
vyjadríme ako preponu v pravouhlom trojuholníku.
3. 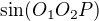 vyjadríme pomocou
vyjadríme pomocou 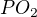 a
a 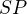 .
.
4. 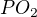 vyjadríme ako preponu v pravouhlom trojuholníku.
vyjadríme ako preponu v pravouhlom trojuholníku.
Možno je to príliš zložitý postup, ale funguje to...
1^6 - 2^6 + 3^6 = 666
Offline


