Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sucet nulovych mnozin (TOTO TÉMA JE VYŘEŠENÉ)
#2 04. 12. 2012 14:33 — Editoval kompik (04. 12. 2012 14:33)
Re: sucet nulovych mnozin
↑ Brano:
Sum of sets of measure zero - MSE
Píšu tam, že Cantorova množina je kontrapríklad, lebo C+C=[0,2].
Predpokladám, že toto by sa malo dať zdôvodniť z reprezentácie Cantorovej množiny v trojkovej sústave. (Aj keď som to zatiaľ neskúšal zdôvodniť detailne. A možno sa to dá aj nejako jednoduchšie.)
Aj táto linka sa zaoberá do istej miery podobným problémom Existence of measure zero generating sets of additive real numbers - MSE.
Offline
#3 04. 12. 2012 15:37
Re: sucet nulovych mnozin
↑ Brano: , ↑ kompik:
Ahoj. To tvrzení o Cantorově diskontinuu je dokázáno v tomto vlákně .
Offline
#4 04. 12. 2012 16:57
Re: sucet nulovych mnozin
↑ kompik:↑ Rumburak:
Dakujem. Dokonca ma napadlo, ze v  pre
pre  to ide este trivialnejsie, konkretne si mozme zobrat lubovolny vektor
to ide este trivialnejsie, konkretne si mozme zobrat lubovolny vektor  a za
a za  zobrat nadrovinu kolmu na
zobrat nadrovinu kolmu na  a za
a za  zobrat priamku rovnobeznu s
zobrat priamku rovnobeznu s  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » sucet nulovych mnozin (TOTO TÉMA JE VYŘEŠENÉ)

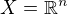 a
a  je vonkajsia Lebesgueova miera na
je vonkajsia Lebesgueova miera na  . Pre
. Pre  definujme
definujme 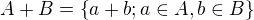 . Ak
. Ak  potom
potom  .
.