Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Počet lineárních rozšíření daného uspořádání konečné množiny. (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 12. 2012 11:11 — Editoval Andrejka3 (05. 12. 2012 11:12)
Počet lineárních rozšíření daného uspořádání konečné množiny.
Dobrý den.
Mějme uspořádanou množinu 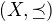 a nechť je
a nechť je  konečná.
konečná.
Kolik lineárních rozšíření  existuje?
existuje?
Neboli, kolik existuje lineárně uspořádaných množin  takových, že
takových, že  ?
?
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 05. 12. 2012 14:37 — Editoval kompik (05. 12. 2012 14:56)
Re: Počet lineárních rozšíření daného uspořádání konečné množiny.
↑ Andrejka3:
Keď som sa Googlu opýtal na "number of linear extensions" poset, tak mi vrátil napríklad takéto odkazy:
* Linear extension - Wikipedia
* Best known bounds for the number of linear extensions of a poset - MSE
Podľa tej literatúry, čo tam je uvedená, sa zdá, že sa okolo takýchto problémov robí nejaká celkom dosť seriózna matika.
A tipoval by som z toho, že asi nejaké úplne jednoduché vyjadrenie nie je. Ak ti teda náhodou nestačí nejaké rekurentné vyjadrenie - napríklad ako je uvedené tu: Paul Edelman, Takayuki Hibi, Richard P. Stanley: A recurrence for linear extensions; Order 1989, Volume 6, Issue 1, pp 15-18, DOI: 10.1007/BF00341632, free link.
EDIT: Aj podľa tohoto sa zdá, že to asi bolo pomerne dosť študované. V Richard P. Stanley: Enumberative combinatorics píšu
If
, then an order-preserving bijection
is called an extension of P to a total order or linear extension of P.
The number of extensions of P to a total order is denotedand is probably the single most useful number for measuring the "complexity" of P.
Offline
#3 05. 12. 2012 16:45 — Editoval Andrejka3 (05. 12. 2012 17:00)
Re: Počet lineárních rozšíření daného uspořádání konečné množiny.
↑ kompik:
Díky, velmi zajímavé!
PS: v tom citovaném by mě zajímalo, v čem konkrétně by ta užitečnost mohla být (jen k měření složitosti?) :)
Díky za Tvůj čas.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 05. 12. 2012 17:50
Re: Počet lineárních rozšíření daného uspořádání konečné množiny.
Andrejka3 napsal(a):
↑ kompik:
PS: v tom citovaném by mě zajímalo, v čem konkrétně by ta užitečnost mohla být (jen k měření složitosti?) :)
O kombinatorike toho viem veľmi málo - sem som skutočne napísal iba to, čo sa mi podarilo vygoogliť. Čiže k tomuto by pomohlo asi jedine zobrať si tú knihu a pozrieť sa, čo v nej s tým e(P) ešte robia. Alebo počkať, či sa tu vyjadrí niekto, kto sa v tejto oblasti vyzná.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Počet lineárních rozšíření daného uspořádání konečné množiny. (TOTO TÉMA JE VYŘEŠENÉ)
