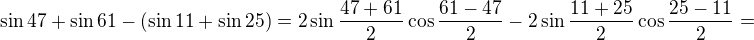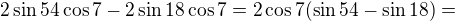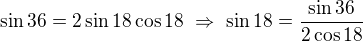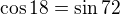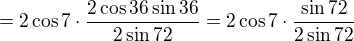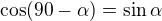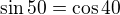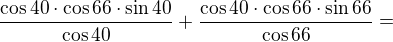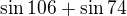Matematické Fórum

010010 · 07. 12. 2012 19:49

b) sin 47° + sin 61° - sin 11° - sin 25° = cos 7°
a) sin 50° sin 24°(tg 40° + tg66°) + sin 74° = 2cos 16°

Dobrý večer. Neviem si rady s týmito príkladmi :/
Použil som súčtové vzorce a potom násobenie sinxcosy ale vždy som sa dostal k pôvodnému zadaniu.
Ďakujem za pomoc.

010010 · 07. 12. 2012 20:47

mám dokázať rovnosť

zdenek1 · 07. 12. 2012 21:42

↑ 010010:
$\sin 47+\sin 61-(\sin 11+\sin 25)=2\sin \frac{47+61}{2}\cos \frac{61-47}{2}-2\sin \frac{11+25}{2}\cos \frac{25-11}{2}=$
$2\sin 54\cos 7-2\sin 18\cos 7=2\cos 7(\sin 54-\sin 18)=$
$2\cos 7\cdot 2\cos \frac{54+18}{2}\sin \frac{54-18}{2}=2\cos 7\cdot 2\cos 36\sin 18$

a nyní vztah pro $\sin2\alpha$
$\sin 36=2\sin 18\cos 18\ \Rightarrow \ \sin 18=\frac{\sin 36}{2\cos 18}$
ale $\cos18=\sin72$
dostáváme
$=2\cos 7\cdot \frac{2\cos 36\sin 36}{2\sin 72}=2\cos 7\cdot \frac{\sin 72}{2\sin 72}$

010010 · 07. 12. 2012 22:26 — Editoval 010010 (07. 12. 2012 23:03)

hmm. Všetkému rozumiem, len nie tomu, ako dostanem ten cos18=sin72

Edit: Už viem :)

Pomôžete mi prosím aj s príkladom b ?

zdenek1 · 07. 12. 2012 23:05

↑ 010010:
$\cos (90-\alpha )=\sin \alpha$

zdenek1 · 07. 12. 2012 23:19

↑ 010010:
úplně stejný trik
$\sin 50=\cos 40$
$\sin24=\cos 66$
a pak
$\frac{\cos 40\cdot \cos 66\cdot \sin 40}{\cos 40}+\frac{\cos 40\cdot \cos 66\cdot \sin 66}{\cos 66}=$
$\cos 66\cdot \sin 40+\cos 40\cdot \sin 66=\sin 106$

a pak
$\sin 106+\sin 74$
už je jen součtový vzorec

010010 · 07. 12. 2012 23:49

zdenek1 napsal(a):
↑ 010010:
úplně stejný trik
$\sin 50=\cos 40$
$\sin24=\cos 66$
a pak
$\frac{\cos 40\cdot \cos 66\cdot \sin 40}{\cos 40}+\frac{\cos 40\cdot \cos 66\cdot \sin 66}{\cos 66}=$
$\cos 66\cdot \sin 40+\cos 40\cdot \sin 66=\sin 106$

a pak
$\sin 106+\sin 74$
už je jen součtový vzorec

Netuším odkiaľ je opäť: +sn74

Ale, už mi to vyšlo, vzhľadom na to, že sin106=sin16 => cos(-16)=sin16 <=> cos16=cos16

Ďakujem :)

zdenek1 · 08. 12. 2012 07:10

↑ 010010:

Netuším odkiaľ je opäť: +sin74

tak si přečti zadání.

cos(-16)=sin16 <=> cos16=cos16

Toto je ale nesmysl.

010010 · 10. 12. 2012 01:00 — Editoval 010010 (10. 12. 2012 01:01)

cos(-16)=sin16 <=> cos16=cos16
Toto je ale nesmysl.

pomýlil som sa :) má byť cos(-16)=cos16

Matematické Fórum

#1 07. 12. 2012 19:49

Goniometria

#2 07. 12. 2012 20:47

Re: Goniometria

#3 07. 12. 2012 21:42

Re: Goniometria

#4 07. 12. 2012 22:26 — Editoval 010010 (07. 12. 2012 23:03)

Re: Goniometria

#5 07. 12. 2012 23:05

Re: Goniometria

#6 07. 12. 2012 23:19

Re: Goniometria

#7 07. 12. 2012 23:49

Re: Goniometria

zdenek1 napsal(a):

#8 08. 12. 2012 07:10

Re: Goniometria

#9 10. 12. 2012 01:00 — Editoval 010010 (10. 12. 2012 01:01)

Re: Goniometria

Zápatí