Matematické Fórum

wescoast · 02. 12. 2008 13:21

Ahoj, potřeboval bych poradit s jednou limitou, vím, že to nebude nic těžkého, potřeboval bych jen popostrčit.

${\lim}\limits_{n \to \infty}\frac{1}{n}\frac{\sqrt[3]{n^3+3n }-\sqrt{n^2-2n }}{\sqrt{n^2+2 }-\sqrt{n^2-2 }}$

Nevím co s tím, když mám v čitateli třetí a druhou odmocninu. Nebo to vynásobit jmenovatelem, ale s + mezi odmocninami?

Děkuji za jakoukoli pomoc.

Pavel · 02. 12. 2008 13:31

↑ wescoast:

Co tak přepsat druhou resp. třetí odmocninu v čitateli na šestou domocninu z třetí resp. druhé mocniny? Pak už to nějak půjde.

wescoast · 02. 12. 2008 14:26

↑ Pavel:

Poradíš jěště prosím. Udělal jsem to, ale nevim jak dál....

math.oaf · 02. 12. 2008 20:30

↑ wescoast:
jedin co ma napadlo:
pouzit vztah: $(a-b)(a^5 +a^4 b^1 +a^3 b^2 ...+ a^0b^5)=a^6 -b^6$ $(*)$
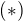
vypocitaj to ako limitu sucinu limit: ${\lim}\limits_{n \to \infty}\frac{1}{n(\sqrt{n^2 +2}-\sqrt{ n^2-2 })}=\frac{1}{2}$ to je klasika a limity ${\lim}\limits_{n \to \infty}\sqrt[3]{n^3+3n }-\sqrt{n^2-2n }$ , na ktoru pouzije spominany vztah, v citateli dostanes
$(n^3 +3n)^2-(n^2 -2n)^3$ , kde n na 6 sa ti vybuší a s najvyssou mocninou bude clen
$6n^5$ , tak teraz uz len menovatel: radsej vyjmi z a,b pred odmocninu n, teda
$a=n\sqrt[3]{1+\frac{3}{n^2 }} , b=n\sqrt[2]{1-\frac{2}{n }}$ no a ked na to pouzijes tu druhu zatvorku z 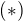$(*)$ budes mat pri kazdom clene $n^5$ to vyjmes pred zatvorku, vybusi sa ti to s citatelom, limita citatela bude 6, a menovatela tiez 6, lebo tam mas sest clenov, pricom kazdy je sucin dvoch odmocnin, ktorych limita je 1, teda vysledna je 1 a konecne celkova limita je 0.5, isto to je dobre overil som to na compe, ale ci to je najlepsi spusob, pochybujem :D

Matematické Fórum

#1 02. 12. 2008 13:21

Iracionální posloupnosti - limita

#2 02. 12. 2008 13:31

Re: Iracionální posloupnosti - limita

#3 02. 12. 2008 14:26

Re: Iracionální posloupnosti - limita

#4 02. 12. 2008 20:30

Re: Iracionální posloupnosti - limita

Zápatí