Matematické Fórum

markesBK · 15. 12. 2011 12:27

zdravim, mam problem s touto ulohou, mal som to nakreslene, ale bolo to zevraj vyriesene len pre konkretny pripad...tak mi bolo povedane, ze tam treba vyuzit tento vztah $|E(G)|\le \frac{V(G)^{2}}{4}$ . Ak by vedel niekto dalej poradit bol by som rad. Diky :)

takto som to mal nejak popisane + obrazok....
Stačí si nakresliť graf, pričom vrcholov bude 9 (počet osôb) a hrany budú reprezentované tým, kto koľko ľudí pozná, teda ak jedna osoba pozná dve iné, potom z jedného vrcholu pôjdu dve hrany k ľubovoľným iným hranám. Po nakreslený grafu už je jasne vidieť cyklus s tromi vrcholmi, čo reprezentuje to, že nejaký traja ľudia sa poznajú navzájom.

uloha: V skupine deviatich osôb jedna osoba pozná dve iné, dve osoby poznajú štyri iné, štyri osoby poznajú päť iných a zvyšné dve osoby poznajú šesť iných. Dokážte, že potom niektoré tri osoby sa poznajú navzájom.

Simonka91 · 15. 12. 2011 12:30

↑ markesBK: nestaci to nakreslit? :)

markesBK · 15. 12. 2011 12:43

↑ Simonka91: nie, pretoze to je len riesenie pre konkretny pripad..

petrkovar · 15. 12. 2011 14:01

↑ markesBK:Předpokládám, že zádrhel je určit $|E(G)|$ , nebo?
Ale vždyť podle principu sudosti je dvojnásobek počtu hran roven součtu stupňů vrcholů v grafu. Stupně vrcholů jsou přímo v zadání...

markesBK · 15. 12. 2011 14:24

↑ petrkovar: no tak napisal som si to takto....od zadu...dve poznaju 6 atd...665555442, takze sucet stupnov vrcholov je 6+6+5+ atd... 32? tak 32=2e, taze e=16? to dosadim vsetko do toho vztahu $|E(G)|\le \frac{V(G)^{2}}{4}$ a ak to bude platit tak co to znamena? ..neviem mne ta teoria grafom velmi nejde :(

petrkovar · 15. 12. 2011 16:49

↑ markesBK:A co vyjde po dosazení do vztahu?

markesBK · 15. 12. 2011 16:54

↑ petrkovar: 64<= 32 na druhu...ak to je dobre...a ako vlastne ukazat, ze tam vznikne ten trojuholnik, ze 3 osoby sa navzajom poznaju...

petrkovar · 15. 12. 2011 20:39

↑ markesBK:Ne, to není dobře dosazeno.
Kolik je $|E(G)|$ a kolik $|V(G)|$ ?

markesBK · 16. 12. 2011 11:17

↑ petrkovar: V(G)=2e nie? cize 32=2e...e= 16... a potom jak som dosadil do toto vztahu tak vyslo 64<= 32 na druhu...ak to je dobre no

petrkovar · 16. 12. 2011 13:08

↑ markesBK:Ne. Jednak je nutnot pečlivě rozlišovat symboliku: $V(G)$ je množina a $|V(G)|$ počet jejích prvků, ale hlavně podle zadání je $|V(G)|=9$ .

rado111

Vedel by mi niekto pomôcť s týmto dôkazom?

Nech k je dĺžka najdlhšej cesty v grafe G. Dokážte, že $\lambda$ (G) $\le$ k+1

Potrebujem to čo najskôr. Potrebujem to dokázať číselne nie graficky.
Skúšala som to hľadať aj na internete a nikde som to nenašla.
Spísala som si k tomu vzorce.
Možno pomôže že vo všeobecnosti platí, že:
$\lambda$ (G) je chromatické číslo, čo najmenej farieb vrcholov, aby hrana obsahovala vrcholy rôznej farby
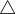$\triangle$ (G) je maximálny stupeň v grafe

petrkovar · 08. 12. 2012 17:54

↑ rado111:Novou otázku, prosím, do nového vlákna. (pravidla)

rado111 · 10. 12. 2012 10:34

nechápem akého vlákna :)

jelena · 10. 12. 2012 22:53

↑ rado111:

nového (tématu). Zdravím.

Matematické Fórum

#1 15. 12. 2011 12:27

teoria grafov

#2 15. 12. 2011 12:30

Re: teoria grafov

#3 15. 12. 2011 12:43

Re: teoria grafov

#4 15. 12. 2011 14:01

Re: teoria grafov

#5 15. 12. 2011 14:24

Re: teoria grafov

#6 15. 12. 2011 16:49

Re: teoria grafov

#7 15. 12. 2011 16:54

Re: teoria grafov

#8 15. 12. 2011 20:39

Re: teoria grafov

#9 16. 12. 2011 11:17

Re: teoria grafov

#10 16. 12. 2011 13:08

Re: teoria grafov

#11 08. 12. 2012 17:43 — Editoval rado111 (08. 12. 2012 17:50)

Re: teoria grafov

#12 08. 12. 2012 17:54

Re: teoria grafov

#13 10. 12. 2012 10:34

Re: teoria grafov

#14 10. 12. 2012 22:53

Re: teoria grafov

Zápatí