Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 12. 2012 04:13
- stuart clark

- Příspěvky: 1015
- Reputace: 7
x,y,z
If  .Then value of
.Then value of  in
in 
Offline
- (téma jako vyřešené označil(a) byk7)
#3 13. 12. 2012 13:32
Re: x,y,z
I belive that solutions are only  and
and  ; note that
; note that  .
.
↑ stuart clark: is this your homework?
Offline
#4 13. 12. 2012 15:04 — Editoval vanok (14. 12. 2012 02:35)
Re: x,y,z
Hi ↑ stuart clark:,
I found two families (very simple) solutions:
 and
and  ,
,  for
for  .
.
However, I do not have, still managed to prove if it exist the other solutions in this case.
So, it is likely that  and
and  are only solutions of your problem (of this type).
are only solutions of your problem (of this type).
Sincerely Vanok.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 13. 12. 2012 22:04 — Editoval vanok (14. 12. 2012 02:41)
Re: x,y,z
Hi ↑ anes:,
Anothers solutions are 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 19. 12. 2012 02:57
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: x,y,z
↑ Brano: This is not my Homework.
actually this is Given in my preparation book.
↑ Tomas.P:↑ vanok:↑ anes:
Thanks
Offline
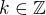 ,
,  (i.e.
(i.e.  ).
).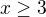 . Then we must have
. Then we must have  so we get an integer on the left hand side; without loss of generality
so we get an integer on the left hand side; without loss of generality  .
. , where both of the fractions at the right have integer values, so necessarily
, where both of the fractions at the right have integer values, so necessarily  and
and  for some
for some  ,
, 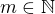 .
. . However,
. However,  would imply
would imply  ,
,  . Considering the equation mod 9, we notice this is impossible. That leaves us with
. Considering the equation mod 9, we notice this is impossible. That leaves us with  .
.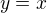 or
or  . And second option is clearly not compatible with a).
. And second option is clearly not compatible with a). . In that case
. In that case  for
for  .
. for any solution of the original problem and we can easily check that the only solutions are
for any solution of the original problem and we can easily check that the only solutions are  ,
,  as vanok points out. Thanks.
as vanok points out. Thanks.