Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dimenze vekt. prostoru (TOTO TÉMA JE VYŘEŠENÉ)
#3 04. 12. 2008 14:26 — Editoval rughar (04. 12. 2008 14:51)
Re: Dimenze vekt. prostoru
↑ wescoast:
Omlouvám se za moji neznalost, ale opravdu jsem se s tím nikde nesetkal a to přestože jsem se setkal už s mnohými formalismy kolem vektorových prostorů. A nikdo jiný na tento příspěvek ani nereaguje.
Když vemeš několik vektorů, svážeš je do hranaté závorky a připíšeš k nim dolní index. Co to je za objekt?
Jinak můj tip je prostě 4. Protože ty vektory jsou z vektorového prostoru dvojce komplexních čísel, který má dimenzi 2×2.
Pokud myslíš toto
Tak to má dimenzi 16. Neboť můžu najít 16 objektů, které jsou lineárně nezávislé





a tak dále. Nevim potom, jak to souvisí s tím konkrétním A). Dimenze je něco, co ukazuje něco jako počet stupňů volnosti daného objektu. Například euklidovský prostor R3 má dimenzi 3, neboť lze do něj vepsat 3 navzájem kolmé vektory. Takže při otázce dimenze nemá smysl se odkazovat na konkrétní vektory.
Možná tou hranatou závorkou myslíš bázi poskládanou ze zadaných vektorů (pak nechápu moc smysl toho indexu lambda). To má zas pro změnu dimenzi 4. Nebo těžko říct, protože jsi nezadal x_4 takže nelze určit, jestli některé z x_1 až x_4 nejsou třeba lineárně závislé.
Teď už ale možná píšu nesmysly ....
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#5 04. 12. 2008 21:26
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dimenze vekt. prostoru
x_1=(1+i, 1-i), x_2=(-4+11i, -1-5i), x_3=(-1+9i, 1-5i),x_4 = (2-3i, 1+i)
Každý vektor má čtyři složky a,b,c,d. Je ale jedno, jestli uvažuju přímo vektor (a+bi,c+di) nebo vekor (a,b,c,d) jeho souřadnic vzhledem k bázi (1,0),(i,0),(0,1),(0,i). Vektory souřadnic našich čtyř vektorů jsou tedy
(1,1,1,-1),(-4,11,-1,-5),(-1,9,1,-5),(2,-3,1,1). Ty je teď potřeba naskládat po sloupcích do matice a určit její hodnost.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dimenze vekt. prostoru (TOTO TÉMA JE VYŘEŠENÉ)
 je soubor vektorů z prostoru
je soubor vektorů z prostoru  nad R. Určete dim
nad R. Určete dim ![kopírovat do textarea $[x_1,x_2,x_3,x_4]_\lambda$](/mathtex/41/4120d9ab8bff7d57e069b209b6875829.gif) , je-li:
, je-li: =(1+i, 1-i),
=(1+i, 1-i),  =(-4+11i, -1-5i),
=(-4+11i, -1-5i), 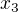 =(-1+9i, 1-5i).
=(-1+9i, 1-5i).