Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 12. 2012 13:47 — Editoval ((:-)) (25. 12. 2012 13:48)
#4 25. 12. 2012 19:22
Re: neceločíselný faktoriál
↑ Honza90:
To ja neviem - možno Ti odpovie niekto s lepšími vedomosťami z tejto problematiky.
Našla som iba toto.
Offline
#5 25. 12. 2012 19:40
Re: neceločíselný faktoriál
↑ Honza90:
Pre počítanie s mocninami s reálnym exponentom platia tie isté pravidlá, ako pre mocniny s racionálnym exponentom.
Napr.  a pod.
a pod.
server.gphmi.sk/~domanyov
Offline
#6 25. 12. 2012 19:50 — Editoval jarrro (11. 08. 2019 23:55)
Re: neceločíselný faktoriál
taká najzákladnejšia konštrukcia je, že sa ukáže, že pre ľubovoľné kladné číslo  a ľubovoľnú konvergentnú postupnosť
a ľubovoľnú konvergentnú postupnosť  racionálnych čísiel hodnota
racionálnych čísiel hodnota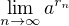 závisí len na limite postupnosti
závisí len na limite postupnosti 
z toho a z faktu, že racionálne čísla sú v reálnych číslach husté
môžeme definovať pre každé reálne číslo  číslo
číslo , kde
, kde  je postupnosť racionálnych čísiel konvergujúca k
je postupnosť racionálnych čísiel konvergujúca k 
MATH IS THE BEST!!!
Offline
#7 25. 12. 2012 23:59
Re: neceločíselný faktoriál
Ahoj. Předpokládám, že se bavíme o hodně jednoduché kalkulačce. Když se člověk koukne na nějakou pokročilejší dnešní, tak to už je skoro normální počítač, na kterém může běžet cokoliv.
U těch jednoduchých kalkulaček jsem si vždy v prvním přiblížení představoval, že má uložených prvních pár členů Taylora, do kterých akorát dosadí. Automaticky člověku dojde, že se možná najdou praktičtější aproximace než Taylor, že by třeba bylo možné předpočítat si nějaké hodnoty a nějak je použít k urychlení a zpřesnění výpočtu atd. Nicméně jako nápad vypadá aproximace pomocí řad celkem použitelně. To by asi taky řešilo otázku, jak se kalkulačka popasuje s iracionálním exponentem (bude jí úplně fuk, prostě ho dosadí do polynomu), a dá se předpokládat, že by se našla i nějaká použitelná řada aproximující tu gama funkci (google vyhazuje třeba "Lanczos approximation"; jestli použitelná nevím, ale nějaká řada to je).
Nicméně to je jen takový nápad, jak si takovou základní kalkulačku naprogramovat na koleně. Jestli se to tak ale opravdu prakticky dělá, nevím. Při rychlém googlení totiž člověk sem tam zavadí o něco ve stylu vyjadřování funkcí pomocí goniometrických (takže Fourierův rozvoj? nebo něco jiného? -- bohužel teď moc nemám čas to zkoumat). Je také možné, že se používají nějaké speciálnější algoritmy šité na míru hardwaru kalkulačky, které člověka od stolu nenapadnou. Z toho pohledu mi přišel zajímavý popis nějakých algoritmů z dob, kdy se šetřilo každým bitem a každou operací, na který jsem narazil tady
http://jacques-laporte.org/TheSecretOfTheAlgorithms.htm
http://jacques-laporte.org/Logarithm_1.htm
Jinak mi je jasné, že můj příspěvek nijak zásadní informaci nenese, tak snad aspoň podnítí nějakou zajímavou diskuzi v tom směru, který, předpokládám, Honza90 zamýšlel. Sice teď nemám čas a moc ani chuť něco k tomu tématu načítat, to ale neznamená, že by mě odpověď někoho znalejšího nezajímala.
Offline
#8 26. 12. 2012 01:41
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: neceločíselný faktoriál
↑ jarrro:
Ahoj, alternativně lze definovat  jako
jako  .
.
"Máte úhel beta." "No to nemám."
Offline
#12 26. 12. 2012 15:56 — Editoval jarrro (26. 12. 2012 16:01)
Re: neceločíselný faktoriál
kedysi sme sa o tom bavili s Olinom pokúsim sa to nájsť
tu je to http://forum.matweb.cz/viewtopic.php?id=20644
ale platí tam pre prirodzený rád len implikácia, že ak existuje štandardná tak existuje aj nová
inak pre záporné celé by sa to tiež mohlo definovať postupným integrovaním
MATH IS THE BEST!!!
Offline

 zajímalo by mě jak toto vypočítá. Provádí se výpočet pomocí gama funkce?
zajímalo by mě jak toto vypočítá. Provádí se výpočet pomocí gama funkce?