Matematické Fórum

Babča · 28. 12. 2012 11:16

Zdravím,prosím o pomoc v řešení tohoto příkladu :

Určete úhel alfa v trojúhelníku ABC,platí-li pro jeho strany :

a) $a^2=b^2+c^2+bc$ , b) $a^2=b^2+c^2-bc$

Díky.

LukasM · 28. 12. 2012 11:39

↑ Babča:
Téma jsi pojmenoval/a "cosinová věta". Co tedy říká cosinová věta, a jak by to tu šlo využít? Stačí porovnat cosinovou větu s tím co máš zadané, a hned vidíš kolik musí být cosinus toho úhlu.

Babča · 28. 12. 2012 13:25

↑ LukasM:↑ LukasM:↑ LukasM:↑ LukasM:

a] a^2 = b^2 + c^2 + bc

b^2 + c^2 - 2bc * cos alpha = b^2 + c^2 -bc

cos alpha = 3bc

Je to tak ??????? Je to výsledek? Neznám pro alfa znak...znaky pro řeckou abecedu.

Posoudíš to,prosím????Díky.

LukasM · 28. 12. 2012 13:37

↑ Babča:
b^2 + c^2 - 2bc * cos alpha = b^2 + c^2 -bc

Tohle je skoro správně, jen na konci nemá být mínus ale plus - tos sem ale asi jen špatně opsala. Horší je ale ta další úprava. Před tím cosinem není plus, ale krát. Takže z toho bude spíš něco jako $-2bc\cdot \cos{\alpha}=bc$ . Z toho by už neměl být problém dopočítat ten úhel.

marnes · 28. 12. 2012 13:40

↑ Babča:
Pracuji dle skvělého návodu LukaseM

$a^2=b^2+c^2+bc$
$a^2=b^2+c^2-2bc\cos \alpha$

porovnáním dostáváme
$bc=-2bc\cos \alpha$
$cos\alpha =-\frac{1}{2}$ a alfa dopočítáme

Rumburak

↑ Babča:

Zdravím také.

Především si uvědom, že a) a b) jsou DVĚ úlohy , každá o jiném trojúhelníku (jinak by muselo platit bc = 0 ,
což strany žádného trojúh. nemohou splňovat).

Vezměme nejprve úlohu a) s rovnicí

(a) $a^2=b^2+c^2+bc$ .

Nyní si vyjádři (podle cosinové věty) 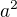$a^2$ pomocí stran $b, c$ a úhlu $\alpha$ a takto získanou rovnici porovněj s (a).

Babča · 28. 12. 2012 15:26

↑ LukasM:

Lukasi,ano...udělala jsem chybu v zadání při opisování.

Výsledky : a) alpha = 120 °

b) alpha = 60 °

Doufám,že teď je to správně....díky za pomoc.

Matematické Fórum

#1 28. 12. 2012 11:16

cosinova věta

#2 28. 12. 2012 11:39

Re: cosinova věta

#3 28. 12. 2012 13:25

Re: cosinova věta

#4 28. 12. 2012 13:37

Re: cosinova věta

#5 28. 12. 2012 13:40

Re: cosinova věta

#6 28. 12. 2012 13:48 — Editoval Rumburak (28. 12. 2012 13:49)

Re: cosinova věta

#7 28. 12. 2012 15:26

Re: cosinova věta

Zápatí