Matematické Fórum

necoPotrebuju · 29. 12. 2012 22:00

Ahoj,

$f_{1}(x,y) = x^{2}+y^{2}-4 = 0$
$f_{2}(x,y) = ln(2-x)-y = 0$

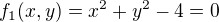
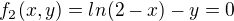
příklad odsud příklad

Uvědomil jsem si, že nerozumím významu nelineární rovnice a rovnice obecně, respektive jak se to dá nakreslit do grafu, protože podle toho se potom volí počáteční aproximace. Ani si nejsem jistý, jak se vyjádřit, co vlastně nechápu. Nechápu prostě smysl rovnice o dvou neznámých. Minulý semestr jsme měli funkce 2 proměnných a tam jsem chápal, že po dosazení libovolných dvou hodnot z R za 'x' a 'y' dostanu bod 'z' a dostanu jakoby bod ve 3D prostoru. To byly ale funkce, které mi vracejí nějakou hodnotu. Jaký je ale význam nelineární rovnice se dvěma neznámými? Nechápu, jak se to dá nakreslit do 2D grafu, jak je to v té prezentaci, co jsem na ni poslal odkaz a už vůbec nechápu, podle čeho se zvolila ta počáteční aproximace [1,2]. Díky za to, že se mnou budete mít trpělivost, nejsem moc inteligentní, vždycky se nějak prokoušu, protože se naučím algoritmus, ale vůbec tomu nerozumím.

jelena · 29. 12. 2012 22:53

Zdravím,

pokud pomůže, můžeš pohlížet na své zápisy jako na funkce zadané implicitně (bez podrobnějšího hloubání, zda skutečně splňuji veškeré podmínky pro implicitní funkce).

Jiný pohled - funkce 2 proměnných je f(x, y)=0 dává průsečík "grafu funkce v prostoru" s rovinou xOy. V každém případě pro zakreslení grafu buď můžeš ze zadané rovnice vyjádřit 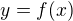$y=f(x)$ - to se stane pro 2. rovnici ze zadání ( 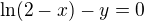$\ln(2-x)-y = 0$ ) nebo zůstat u implicitního zápisu a vybavit si rovnice např. kuželoseček $x^{2}+y^{2}=4$ - je co? Stačí tak pro zorientování? Děkuji.

necoPotrebuju · 29. 12. 2012 23:11

jelena napsal(a):
Zdravím,

pokud pomůže, můžeš pohlížet na své zápisy jako na funkce zadané implicitně (bez podrobnějšího hloubání, zda skutečně splňuji veškeré podmínky pro implicitní funkce).

Jiný pohled - funkce 2 proměnných je f(x, y)=0 dává průsečík "grafu funkce v prostoru" s rovinou xOy. V každém případě pro zakreslení grafu buď můžeš ze zadané rovnice vyjádřit $y=f(x)$ - to se stane pro 2. rovnici ze zadání ( $\ln(2-x)-y = 0$ ) nebo zůstat u implicitního zápisu a vybavit si rovnice např. kuželoseček $x^{2}+y^{2}=4$ - je co? Stačí tak pro zorientování? Děkuji.

Jo dík, už je mi to jasnější, ale stejně nechápu, proč je ta počáteční aproximace zvolena [1,2], vždyť ten bod je daleko od nějakého průsečíku těch dvou funkcí. Nevíš pls?

jelena · 29. 12. 2012 23:42

↑ necoPotrebuju:

pokud si počteš podrobnější materiály z numerických metod, potom zrovna u soustav nelineárních rovnic se považuje za obtížné volba počátečního bodu a odhad, zda metoda bude úspěšně konvergovat. Vychází se z posouzení situace (zejména, pokud bys řešil něco praktického bez použití počítače, tak můžeš odhadnout, do kterých hodnot může být výsledek).

Konkrétně zde je jasné, že nemůžeš se vzdalovat od kružnice s poloměrem r=2 ani ven, ani dovnitř, jelikož výsledek určitě na kružnici leží. Také se můžeš postavit tak, abys v dalším kroku buď přibližoval k jednomu, nebo k druhému kořenu. Což se mi jeví z bodu [1,2] jako dobrá strategická pozice. Nakonec v samotném Tvém odkazu je úloha přímo postavena na zadání počátečního bodu (tedy ho neodhaduješ a jen plníš úkol).

Můžeš samozřejmě prozkoušet i jiný výchozí bod.

Matematické Fórum

#1 29. 12. 2012 22:00

Newtonova metoda pro řešení soustavy nelineárních rovnic

#2 29. 12. 2012 22:53

Re: Newtonova metoda pro řešení soustavy nelineárních rovnic

#3 29. 12. 2012 23:11

Re: Newtonova metoda pro řešení soustavy nelineárních rovnic

jelena napsal(a):

#4 29. 12. 2012 23:42

Re: Newtonova metoda pro řešení soustavy nelineárních rovnic

Zápatí