Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 12. 2012 14:30
a^3 + b^3 = c^2
zdravím všechny, už dávno jsem někde viděl zadání příkladu, ve kterém mám najít všechna kladná celočíselná řešení rovnice 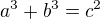 . Já vím že to asi nevyřeším, já jsem jen trochu tuto rovnici upravoval, protože sem se nudil, ale už sem se do toho docela zamotal a nevím jestli to mám zatím dobře. (taká by mě zajímalo jak se této rovnici říká, ale nevím co mám hledat tak sem nic nenašel). prosím tedy jen někoho, komu by se můj postup chtělo číst o kontrolu (nemám to do školy, ani nečekám že to vyřeším, jen by mě zajímalo je mé řešení správné nebo ne)
. Já vím že to asi nevyřeším, já jsem jen trochu tuto rovnici upravoval, protože sem se nudil, ale už sem se do toho docela zamotal a nevím jestli to mám zatím dobře. (taká by mě zajímalo jak se této rovnici říká, ale nevím co mám hledat tak sem nic nenašel). prosím tedy jen někoho, komu by se můj postup chtělo číst o kontrolu (nemám to do školy, ani nečekám že to vyřeším, jen by mě zajímalo je mé řešení správné nebo ne)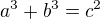 Označím největší společny dělitel čísel a, b jako D. Potom platí:
Označím největší společny dělitel čísel a, b jako D. Potom platí: 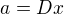 a
a 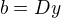 pro nějaká navzájem nesoudělná čísla x a y. Po dosazení máme tvar rovnice:
pro nějaká navzájem nesoudělná čísla x a y. Po dosazení máme tvar rovnice: Teď označím D(D,c) jako E. Platí tedy
Teď označím D(D,c) jako E. Platí tedy  a
a  pro nesoudělná z a F.
pro nesoudělná z a F.
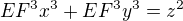 Odsud plyne, že
Odsud plyne, že  dělí
dělí  . Ale F a z jsou nesoudělná. Platí tedy, že
. Ale F a z jsou nesoudělná. Platí tedy, že  . Z této rovnosti přímo vyplívá také rovnost
. Z této rovnosti přímo vyplívá také rovnost  a z ní:
a z ní:  . Připomeňme, že platí také rovnosti
. Připomeňme, že platí také rovnosti 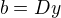 a
a 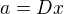 .
.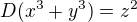 Označme nejvetsi spolecny delitel cisel D a z jako G. Potom platí rovnosti
Označme nejvetsi spolecny delitel cisel D a z jako G. Potom platí rovnosti 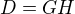 a
a  pro nesoudělná H a d. Nyní platí rovnosti
pro nesoudělná H a d. Nyní platí rovnosti 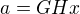 ,
,  a
a 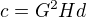 .
.
po dosazení mám: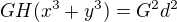

H dělí levou stranu, musí tedy dělit i pravou. Vzhledem k tomu, že d a H jsou nesoudělná, můžou nastat tyto tři možnosti:
a) d = 1; => z = G
b) H = 1; => D = G
c) H dělí G.
Pozn. nevím jestli to mám dobře dosud, ale teprve teď sjem se do toho asi pořádně zamotal, nemám rád větvení příkladu. Jako první jsem zkusil první možnost, potom i druhou, ale v papírech s poznámkami mám docela zmatek. pokusím se naznačit jak sem pokračoval dál:
a) 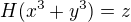 přičemž rovnosti
přičemž rovnosti 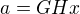 ,
,  a
a 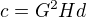 se zjednodušší na tvary
se zjednodušší na tvary  ,
, 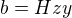 ,
, 
H dělí z, platí tedy 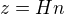 pro nějaké
pro nějaké  . dále platí rovnosti
. dále platí rovnosti  ,
, 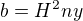 ,
, 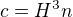 a rovnost
a rovnost 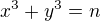
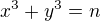 Do rovností pro a,b,c dosadím tuto hodnotu za n:
Do rovností pro a,b,c dosadím tuto hodnotu za n:
Dosadím do zadání hodnoty za a,b,c:

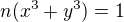

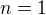
čísla, která poté vyhovují podmínce  a jsou kladná celočíselná, neexistují, tedy aby d=1
a jsou kladná celočíselná, neexistují, tedy aby d=1
- tak to je vše co jsem teď zvládl posbírat z mých papírů. jestli to někdo dočetl až do konce, děkuji, rád bych jen věděl, jestli je můj postup matematicky správný, a také jestli sem někde neudělal chybu. Já podobným způsobem rozebírám i třeba velkou fermatovu větu, a podobně, a pořád si nejsem jistý jestli je to správný postup nebo ne. Za každou odpověď bych byl vděčný.
- pozn. nevím moc do jaké sekce bych měl toto téma zařadit, jako středoškolák sem jej vložil do sekce střední škola. jestli tu nemá co dělat pak prosím o přesunutí
Offline
- (téma jako vyřešené označil(a) liamlim)
#2 31. 12. 2012 15:50 — Editoval liamlim (31. 12. 2012 15:53)
Re: a^3 + b^3 = c^2
teď jsem zkoušel možnost c) tedy že H dělí G, a jsem docela zmatený, něco mi vyšlo a já vůbec nevím co to má znamenat. Navíc jsem si už skoro jistý že jsem někde udělal chybu (prosím někoho aby na ni upozornil). vyšlo mi něco takoveho: - vím, že H dělí G. platí tedy rovnost
- vím, že H dělí G. platí tedy rovnost 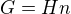 pro nějaké n. po dosazení a vydělení má rovnice tvar:
pro nějaké n. po dosazení a vydělení má rovnice tvar: 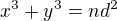 zároveň platí
zároveň platí  ,
, 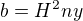 ,
, 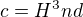 . Po dosazení těchto hodnot do zadání mám rovnici:
. Po dosazení těchto hodnot do zadání mám rovnici: 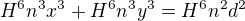 neboli
neboli platí tedy rovnost
platí tedy rovnost 
po uprave platí: 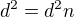 neboli
neboli 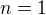 . Po dosazení do rovnice
. Po dosazení do rovnice 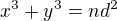 obdržím rovnici
obdržím rovnici 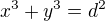 . a ted sem skoncil co s tim? vždyť teď bych mohl celý postup opakovat uplne od zacatku. určitě mám někde chybu, ale kde?
. a ted sem skoncil co s tim? vždyť teď bych mohl celý postup opakovat uplne od zacatku. určitě mám někde chybu, ale kde?
edit: ted se divam, teoreticky by zadani mely vyhovovat vsechny 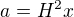 ,
, 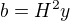 a
a 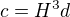 , které vyhovují rovnici
, které vyhovují rovnici 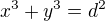 . no ale to je zase nesmysl, protože úplně stejně můžu vyjádřit i x, y a d.
. no ale to je zase nesmysl, protože úplně stejně můžu vyjádřit i x, y a d.
Offline
#4 31. 12. 2012 22:43 — Editoval Mathbrer (31. 12. 2012 22:46)
Re: a^3 + b^3 = c^2
Ted sem na mobilu a nemůžu bohužel moc podrobne napsat co me napadlo. V jak budu moct a vzpomenu si tak tento příspěvek upravím. Děkuji za odpověď, ale i když je v podstatě stejný jako v mem případe. Stačí když zvolime x=1, y=2, d=3. Protoze tyto hodnoty odpovídají i rovnici x3+y3=d2. Asi sem to napsal moc zmatene V jak se dostanu domu napíšu to čitelněji. Mimochodem vse nejlepší všem do nového roku, snad plného radosti z matematiky....
Btw napsal jsem z účtu který mám na mobilu společne s kamarády. Jsem jedna a ta sama osoba snad sem vás moc nezmatl
Offline
#5 01. 01. 2013 01:08 — Editoval Kondr (01. 01. 2013 01:15)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: a^3 + b^3 = c^2
Šikovné bylo to převést na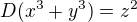 . Pak
. Pak
* x a y zvolíme libovolně
*  lze právě jedním způsobem zapsat jako r^2s, kde s není dělitelné druhou mocninou
lze právě jedním způsobem zapsat jako r^2s, kde s není dělitelné druhou mocninou
* položíme  , kde
, kde  je libovolné, pak
je libovolné, pak 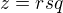 ,
, 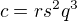 ,
, 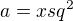 ,
, 
Snadno rozmyslíme, že takto jsme popsali všechna řešení, nejde ale o uzavřený tvar.
U úloh tohoto typu lze často použít nekonečný sestup -- předpokládáme, že máme řešení, které je nejmenší a najdeme menší (pojem "menší" si definujeme jak se nám zlíbí).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#6 01. 01. 2013 01:18
Re: a^3 + b^3 = c^2
Kondr, moc děkuji za vysvětlení, můžu se prosím jen zeptat, co znamená uzavřený tvar? ještě sem to neslyšel, ve škole sme to nebrali (sexta) a nečetl sem to nikde (nebo si nevzpominam). urcite to bude neco jednoducheho, ale nevim...
Offline
#7 01. 01. 2013 01:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: a^3 + b^3 = c^2
Uzavřený tvar je vyjádření výsledku pomocí běžných operací (sčítání, násobení, http://en.wikipedia.org/wiki/Euler%27s_totient_function ...), nevím, jestli je ustálené, jaké funkce se smí použít. Výše uvedené řešení by šlo zapsat pomocí funkce "nejvyšší druhá mocnina dělící X", což za uzavřený tvar nepovažuji.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
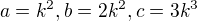 ,pro
,pro