Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergentní či divergentní d'Alembert (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 01. 2013 14:24
Konvergentní či divergentní d'Alembert
Ahoj, dostal jsem se asi k nejtěžší látce co se učím na opravky,
Prosím o pomoc jak na tento příklad.
Mám vypočítat limitu? Nebo co vůbec s tím?
Střelil bych to od oka, ale to prý nestačí :D :-)
Díky za rady.
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
- (téma jako vyřešené označil(a) PanTau)
#3 02. 01. 2013 09:42
Re: Konvergentní či divergentní d'Alembert
↑ Tomas.P:
Děkuji za tvou pohotovou odpověď.
Je mi to jasné, mohl bys mi prosím ještě ukázkově rozepsat tento příklad? Ostatní co budu počítat jsou podobné (ať se mám čeho držet) - díky
(nemusí být komentáře)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#5 02. 01. 2013 10:26
Re: Konvergentní či divergentní d'Alembert
Rumburak napsal(a):
↑ PanTau:
Ahoj. Neboj se zkusit to sám. I zde je to lehké a jeden vzorový příklad už máš.
Kdybys napsal triviální, byl bys jako náš profesor.
Dostal jsem se jen k: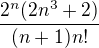
a již nevím co dál /
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#6 02. 01. 2013 10:43 — Editoval Tomas.P (02. 01. 2013 10:43)
Re: Konvergentní či divergentní d'Alembert
↑ PanTau:
Dostal jsem se k ![kopírovat do textarea $\frac{2\[\(n+1\)^3+1\]}{(n+2)(n^3+1)}=\frac{n(2n+2)+2}{(n^3+1)}$](/mathtex/6c/6c39714d548177d983ac21d5554686b5.gif) (viz. Alternate forms).
(viz. Alternate forms).
Offline
#8 02. 01. 2013 10:57
Re: Konvergentní či divergentní d'Alembert
Oh, to je strašně náročne O_o, snad to nějak zvládnu, více méně jsem to pochopil, ale nenapadají mě hned ty matematické upravy.
(mám matiku jen v prvním semestru) ffffffff :-)
Díky za rady a Váš čas.
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#10 02. 01. 2013 11:06
Re: Konvergentní či divergentní d'Alembert
↑ Rumburak:
Spiš určitě než zřejmě, nevěděl jsem například že mám počítat an+1, a počítal jsem pouze an...
Teď co jste mi to vysvětlili je mi to jasné, teď to musím jen na trénovat :-)
Díky
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#12 02. 01. 2013 11:15
Re: Konvergentní či divergentní d'Alembert
↑ Rumburak:
Tj. Konverguje :-)
Díky
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#13 02. 01. 2013 12:17
Re: Konvergentní či divergentní d'Alembert
TECHNICKÝ DOTAZ: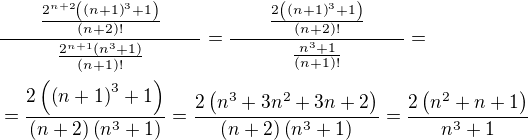
Má být po každé závorce napsáno 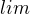 ?
?
Za to nám odečítají body (žádné nedávají!)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#14 02. 01. 2013 13:00 — Editoval jarrro (02. 01. 2013 13:01)
Re: Konvergentní či divergentní d'Alembert
buď všade alebo nikde určite nepíš napr.
alebo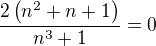
lebo to nie je pravda.
môžeš ale niekde vedľa napísať všetky úpravy bez limity a potom písať nezávisle na tých pomocných výpočtoch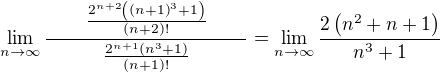
MATH IS THE BEST!!!
Offline
#15 02. 01. 2013 13:23
Re: Konvergentní či divergentní d'Alembert
↑ jarrro:
Díky, zkoušel jsem vypočítat následující příklad:
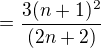
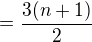
Nechápu proč mi nevyšel, mohl by ses podívat, kde jsem udělal chybu?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#17 02. 01. 2013 13:35
Re: Konvergentní či divergentní d'Alembert
jarrro napsal(a):
Jakto k čeru, však přičitám jedničku? Tak 2 a né 3?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konvergentní či divergentní d'Alembert (TOTO TÉMA JE VYŘEŠENÉ)


![kopírovat do textarea $\frac{a_{n+1}}{a_n}=\frac{[2(n+1)]!}{[(n+1)!]^2}{\cdot}\frac{(n!)^2}{(2n)!}=\frac{[(2n+2)(2n+1)(2n)!]}{[(n+1)(n)!]^2}{\cdot}\frac{(n!)^2}{(2n)!}=\frac{(2n+2)(2n+1)}{(n+1)^2}=\frac{2(n+1)(2n+1)}{(n+1)^2}=\frac{2(2n+1)}{n+1}$](/mathtex/d2/d2f2b8af3b91f13ead7fb5dc731d2ca2.gif)
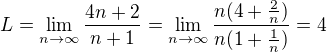
 , tak řada diverguje.
, tak řada diverguje.
 , potom
, potom 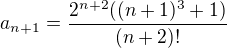 , takže
, takže
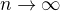 .
. ,
, 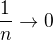 .
.
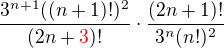
 , proto tam mělo být
, proto tam mělo být 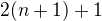 , což je po úpravě
, což je po úpravě 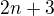 .
.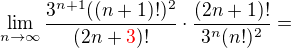 mne táto limita vychádza takto:
mne táto limita vychádza takto: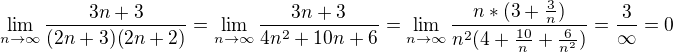 čo robím zle keď mi to nevychádza? ďakujem
čo robím zle keď mi to nevychádza? ďakujem .
. .
.