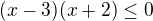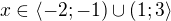Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 01. 2013 12:27
- 010010

- Příspěvky: 82
Logaritmicka nerovnica
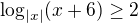
Podmienky:
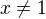
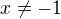

Po prerátaní mi vyšlo: 
Je to správne ?
Pretože keď počítam interval, kde základ logaritmu je medzi 0 a 1, tak po zmenení znamienka mi vychádza opačný interval. A teda riešenie by podľa toho malo byť, že x nepatri len číslam v podmienke.
Ďakujem
Offline
- (téma jako vyřešené označil(a) 010010)
#3 03. 01. 2013 13:34
- 010010

- Příspěvky: 82
Re: Logaritmicka nerovnica
↑ zdenek1:
Takže v a) 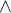 b), robím prieniky definičného oboru(podmienky) s výsledkom danej časti ?
b), robím prieniky definičného oboru(podmienky) s výsledkom danej časti ?
Offline
#5 03. 01. 2013 15:12 — Editoval 010010 (03. 01. 2013 15:36)
- 010010

- Příspěvky: 82
Re: Logaritmicka nerovnica
↑ zdenek1:
Takže budem postupovať podobne ako Vy, v predchádzajúcom príklade.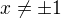



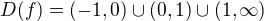
I.)
Mi vyšlo že: 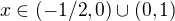
II.)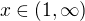
Mi vyšlo že: 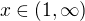
Výsledok: 
Mám to dobre, teda som pochopil správne ten postup ?
EDIT
OPRAVA: výsledok je 
pomýlil som sa v porovnávacom znamienku
Offline
#7 03. 01. 2013 15:39
- 010010

- Příspěvky: 82
Re: Logaritmicka nerovnica
↑ zdenek1:
Áno áno, presne. Už som si to všimol takže výsledok bude podľa toho, kde som sa opravil áno ?
Príklady mám od kamaráta, a ten neviem odkiaľ ich má.
Offline
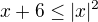
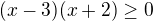

 ,
,