Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 01. 2013 16:21
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Integrál
Čaute, mám tu integrál, ako sa má počítať to "a", to je ako číslo? alebo čo?
Diky :)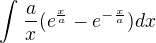
Offline
#3 02. 01. 2013 16:54
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Integrál
Ale vo výsledku je a^2/x(.....) , lenže keď si ja dosadím za "a" napr. 3 tak budem mať integral 3/x (.....) a to keď zintegrujem ostanem 3 * lnx * (......) a nie 9/x * (.....)
Offline
#5 03. 01. 2013 10:35
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Integrál
A ako to mám počítať? metódou Per partes? Neviem začať. Mohol by si mi poradiť? Ďakujem
Offline
#6 03. 01. 2013 22:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
↑ Zlatohlavok:
Zdravím,
nezdá se mi, že by Tvé zadání bylo integrovatelné "běžné metodou" a navíc sedělo k náznaku výsledku, co uvádíš.
a^2/x(.....)
.
Zkus ještě, prosím, překontrolovat zadání a napsat celý výsledek. Děkuji.
Offline
