Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vlastnosti zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#3 06. 01. 2013 14:26
Re: vlastnosti zobrazení
↑ lpfm:
Ahoj. Pokud víš, co ty pojmy znamenají, stačí vyjít z definice.
Asi bys mohl okamžitě rozhodnout o speciálním případu, kdy 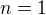 ?
?
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 06. 01. 2013 14:35
Re: vlastnosti zobrazení
↑ Andrejka3:
právě že nevím, potřeboval bych to rozebrat polopaticky, nejlépe na dosazení konkrétních hodnot. :-)
Offline
#5 06. 01. 2013 14:39 — Editoval anes (06. 01. 2013 14:40)
Re: vlastnosti zobrazení
Ahoj, tohle nestačí?
http://cs.wikipedia.org/wiki/Zobrazení_na
http://cs.wikipedia.org/wiki/Injekce_(matematika)
http://cs.wikipedia.org/wiki/Bijekce
... je tam i příklad.
Offline
#6 06. 01. 2013 14:46
Re: vlastnosti zobrazení
Ach ano.
Injekce: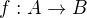 injekce (prostá), právě když
injekce (prostá), právě když  .
.
Do každého prvku množiny B vede nejvýše jedna šipka.
Surjekce = zobrazení na.
Do každého prvku mn. B vede aspoň jedna šipka.
Bijekce = vzájemně jednoznačné
Surjekce a injekce zároveň.
Do každého bodu mn. B vede právě jedna šipka.
To by bylo polopaticky. Stačí použít google, budou-li nejasnosti.
Příklad: , pak
, pak 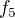 není injekce, protože například
není injekce, protože například  , tedy dva různé prvky
, tedy dva různé prvky  mají stejné obrazy, neboli existuje prvek množiny
mají stejné obrazy, neboli existuje prvek množiny  (nula například), do které vedou aspoň dvě šipky (množina všech jejích vzorů je aspoň dvouprvková).
(nula například), do které vedou aspoň dvě šipky (množina všech jejích vzorů je aspoň dvouprvková).
Pojem šipka je intuitivní :)
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vlastnosti zobrazení (TOTO TÉMA JE VYŘEŠENÉ)

