Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vnoření spočetné lineárně usp. mn. do Q (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 01. 2013 22:15
Vnoření spočetné lineárně usp. mn. do Q
Dobrý den.
Kde  je uspořádaná obvykle.
je uspořádaná obvykle.
Nevím si rady, prosím o nápovědu. Díky.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 07. 01. 2013 12:52 — Editoval Andrejka3 (07. 01. 2013 13:01)
Re: Vnoření spočetné lineárně usp. mn. do Q
Existuje bijekce  .
.
Definuji 
 ,
,
Dále zavedu  , kde
, kde  ,
, ,
,  ,
, zúžení
zúžení  na
na  .
.
Teď mohu pokračovat v konstrukci  rekurzí:
rekurzí:
Uznávám, že je to škaredě zapsané. Je aspoň idea dobrá?
Mimochodem, též znamená, že
též znamená, že  .
.
Edit: Idea je taková, že když další prvek je z dosud zobrazených největší, pak ho zobrazím na číslo o jedna větší než dosavadní největší prvek v množině obrazů, podobně když je nejmenší tak jej zobrazím na číslo o jedna menší než dosavadní nejmenší prvek v množině obrazů, a když ani jedno, tak ho vklíním mezi "sousedy".
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 07. 01. 2013 14:02
Re: Vnoření spočetné lineárně usp. mn. do Q
Je to docela jednoduché, nevím, v čem byl problém. Níže je trochu hezčí zápis.
Pojmenujme naše budoucí vnoření jako  . Pro
. Pro 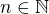 označme
označme  a analogicky
a analogicky  . Dále se bude hodit
. Dále se bude hodit  a
a  .
.

What does a drowning number theorist say?
'log log log log ...'
Offline
#4 09. 01. 2013 12:43 — Editoval kompik (09. 01. 2013 12:55)
Re: Vnoření spočetné lineárně usp. mn. do Q
Andrejka3 napsal(a):
Dále se bude hodit
a
.
Odkiaľ vieme, že to maximum a minimum existuje. (Napríklad keby išlo o dobre usporiadanú množinu, tak by sme mali zaručenú existenciu minima pre každú neprázdnu podmnožinu, ak som správne pochopil, zadanie hovorí o ľubovoľnej lineárne usporiadanej množine.)
EDIT: Tak som si teraz uvedomil, že moja námietka je úplná blbosť. (Mal som si poriadnejšie prečítať to riešenie.)
Existencia minima a maxima je zaručená tým, že množiny 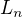 a
a 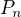 sú konečné.
sú konečné.
Každopádne je to dosť prekvapivý výsledok. (Prinajmenšom na prvý pohľad.)
Offline
#5 09. 01. 2013 12:54 Příspěvek uživatele Andrejka3 byl skryt uživatelem Andrejka3. Důvod: nadbytečné
#6 09. 01. 2013 12:59
Re: Vnoření spočetné lineárně usp. mn. do Q
↑ kompik:
Ano, asi proto mě to zezačátku brzdilo, že tam je takový poloparadox, že se v nekonečnu hezké uspořádání může zmršit na nějaké obludné lineární uspořádání.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vnoření spočetné lineárně usp. mn. do Q (TOTO TÉMA JE VYŘEŠENÉ)
