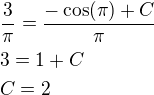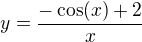Matematické Fórum

O.o · 04. 12. 2008 21:47 — Editoval O.o (04. 12. 2008 21:56)

Ahoj :),

mám tu nějaké problémy a tak trochu nevím, jak dál. Mohl bych Vás prosím požádat o pomoc?
Chyběl jsem na látku dif. rovnic, tak se to snažím do hlavy nějak nasypat přes skripta.

$a) \ \frac{1+y^2}{1+x^2}+y'=0, \ y(- \frac{\sqrt{3}}{3}) = \sqrt{3} \nl vysl: \ y=tg(\frac{\pi}{6}-arctg(x)), x \in (- \sqrt{3}, oo) \nl b) \ y' + \frac{y}{x}=\frac{sinx}{x}, \ y( \pi )= \frac{3}{\pi} \nl vysl: \ y=\frac{1}{x}(2-cosx), x \in (0; oo) \nl c) y'-sinx=3x^2 \nl vysl: \ y=x^3-cosx+C, C \in R, x \in R$

Add a) - řešil jsem asi takto:

$y'= - \frac{1+y^2}{1+x^2} \nl g(x) = -(1+x^2)^{-1}, \ h(y) = 1+y^2 \nl D(g) = R; \ D(h) = R \nl Konstantni \ reseni \ (h(y)=0) \ neni. \nl Podle \ PP \ jsem \ hledal \ obdelnik, \ kde \ najit \ reseni: \nl Reseni \ lezi \ v \ obdelniku: \ O=(-oo; oo)x(0; oo) \nl Tady \ jsem \ si \ nebyl \ jist, \ zda-li \ nemela \ byt \ prva \ cast \ obdelniku \ (-oo; 0)? \nl$

Dále jsem pokračoval separací:

$\frac{dy}{dx}=-\frac{1+y^2}{1+x^2} \nl \int {\frac{1}{1+y^2}dy}=- \int{\frac{1}{1+x^2}dx} \nl arctg(y)=-arctg(x)+C \nl y=tg[C-arctg(x)] \nl$

- Teď nevím, doufám, že to nepletu, ale tahle část je obecným řešením nebo až po dosazení za C? Mám trochu chaos mezi partikulárním řešením a obecným řešením.

$Dosazeni \ PP: \nl \sqrt{3}=tg[c-arctg(\frac{- \sqrt{3}}{3})] \nl arctg(\sqrt{3})=-arctg(\frac{- \sqrt{3}}{3})+C \nl C=\frac{1}{6} \pi \nl y(x)=tg[-arctg(x) + \frac{1}{6} \pi]$

- Tohle si myslím, že je partikulárním řešení, ale říkám, mám v tom trochu chaos.

- Teď mám problém s výsledky, podle výsledků je toto řešení správné, ale ještě tam mají podmínku $x \in (-\sqrt{3}; oo)$ . U této podmínky netuším, jak na ni přišli. Můj tip je nějaký průnik z def. oboru tg, arctg a obdelníku, kde hledáme řešení, ale nejsem si tím vůbec jistý a už vůbec nevím, jak bych to dohromady složil.

Teď se přiznám, že u toho za b) a c) jsem se nedostal nikam. Nějak z těch skritp nechápu, jak mám řešit NLDR (nehomogenní ...). Jediné co jsem z toho psotřehl je, že bych měl nějak řešit nejprve HLDR, řešením nakonec té původní funkce by měl být jakýsi součet partikulárního řešení a řešení HLDR. Nemohl bych Vás požádat, jestli byste mne alespoň nenavedli u prvého příkladu (rád bych to nějak zvládl vyřešit, ale musím říct, že v tom mám strašný zmatek)?
Druhý bych rád zkusil sám, ale postnul jsem ho sem, jestli by nebyl někdo, tak laskavý a pak mi to nezkontroloval?

Děkuji předem za jakoukoli pomoc.

EDIT:
Omlouvám se az psaní nekonečna jako oo a ne \infty.
PP - Počáteční Podmínka
Určit mám obecná (partikulární) řešení.

lukaszh · 04. 12. 2008 21:55

Poradím ti tretí:-)

O.o · 04. 12. 2008 21:58

↑ lukaszh:

Ahoj :),

to jsem si nevybral zrovna dobrý příklad, na kterém bych si to vyzkoušel :)

Jinak samozřejmě díky. Jen snad otázka, tohle je tedy obecné řešení této dif. rovnice, že?

lukaszh · 04. 12. 2008 22:01

↑ O.o:
Myslím, že áno. Vieš ja som ešte diferenciálne rovnice nemal. To len tak, čo som sa naučil po mimo :-) Dík za príklad. Ja viem iba tie ľahké :-)

kaja.marik · 04. 12. 2008 22:45

ad c) vypocita se y' a normalne se to zintegruje

ad b) linearni diferencialni rovnice - jeji reseni je popsano na spouste mist a da se na ni pouzit i MAW (teda aspon na to obecne reseni)

O.o · 06. 12. 2008 08:12

Díky moc.

ttopi · 06. 12. 2008 09:54

Tu 2. si střihnu z cvičných důvodů. Teď to taky bereme a rád si to zkusím.

$y\prime+\frac{y}{x}=\frac{\sin(x)}{x}$

1.Položíme $q=0$

$y\prime=-\frac{y}{x}\nl\frac{dy}{y}=-\frac{1}{x}\ dx\nl \ln|y|+C_1=-\ln|x|+C_2\nl y=e^{-\ln|x|}\cdot e^{C_2-C_1}\nly=\frac{1}{x}K$

2.Variace konstanty
$y=\frac{1}{x}K(x)\nl y\prime=\frac{-1}{x^2}K+\frac{1}{x}K\prime$

Dosadím do původního zadání
$\frac{-1}{x^2}K+\frac{1}{x}K\prime+\frac{K}{x^2}=\frac{\sin(x)}{x}\nl \frac{K\prime}{x}=\frac{\sin(x)}{x}\nlK\prime=\sin(x)\nlK=-\cos(x)+C\nl\rightarrow y=\frac{-\cos(x)+C}{x}$

Požadavek na hodnotu v bodě $\pi$ - $\frac{3}{\pi}=\frac{-\cos(\pi)+C}{\pi}\nl3=1+C\nlC=2$

Řešením je tedy: $y=\frac{-\cos(x)+2}{x}$

kaja.marik · 08. 12. 2008 07:50

↑ O.o:
Kdyz se nakresli graf te funkce tak jde videt, ze funkce tan(pi/6-atan(x)) ma v -sqrt(3) svislou asymptotu. Proto se reseni neda prodlouzit dal doleva.

nekam (http://forum.matweb.cz/viewtopic.php?id=5281) jsem psal, ze reseni diferencialni rovnice muze bud skoncit na kraji oblasti, kde jsou nase funkce se kteryma pracujeme spojitte, anebo tak, ze reseni v konecnem case utece do nekonecna. Ted nastal ten druhy pripad.

Tak snad to ted uz pomoze.

O.o · 08. 12. 2008 18:18

↑ kaja.marik:

Ahoj :),

díky moc, ač jsem překvapený z další odpovědi.
Ještě jednou děkuji

Matematické Fórum

#1 04. 12. 2008 21:47 — Editoval O.o (04. 12. 2008 21:56)

Diferenciální rovnice

#2 04. 12. 2008 21:55

Re: Diferenciální rovnice

#3 04. 12. 2008 21:58

Re: Diferenciální rovnice

#4 04. 12. 2008 22:01

Re: Diferenciální rovnice

#5 04. 12. 2008 22:45

Re: Diferenciální rovnice

#6 06. 12. 2008 08:12

Re: Diferenciální rovnice

#7 06. 12. 2008 09:54

Re: Diferenciální rovnice

#8 08. 12. 2008 07:50

Re: Diferenciální rovnice

#9 08. 12. 2008 18:18

Re: Diferenciální rovnice

Zápatí