Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 01. 2013 12:44 — Editoval APavlat (12. 01. 2013 13:12)
limita
Dobrý den,
nedaří se mi jedna limita, asi neznalostí hyperbolických fcí.
upravim si na:

první zlomek roven jedné, s tím druhým nevím, co dělat... má vyjít 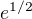 . Díky za odpovědi.
. Díky za odpovědi.
RE.: Vážně si muim rozepisovat tu hyperbolickou fci na exponenciály?...
Offline
- (téma jako vyřešené označil(a) APavlat)


 =
=
 ide do 1.
ide do 1. 


 a vďaka
a vďaka 
