Matematické Fórum

jardofpr · 12. 01. 2013 16:01

Ahojte

potreboval by som pomôcť s jedným príkladom:

Nech $A(t),B(t),C(t),D(t)$ sú spojité maticové funkcie z uzavretého intervalu $I\subset \mathbb{R}$ do $\mathbb{R}^{n\times n}$ .

a) Riešte systém $\begin{array}{ccccc} \frac{\mathrm{d}}{\mathrm{d}t}X &=&AX&+&BY \\ \frac{\mathrm{d}}{\mathrm{d}t}Y &=&CX&+&DY\end{array}$ a určte dimenziu priestoru riešení tohto systému

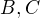b) Nech $tr(A)=0\,,\, D=0$ a $B,C$ sú konštantné matice. Nech 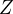$Z$ je nesingulárne maticové riešenie príslušného lineárneho systému z a) . Dokážte, že $\det{\bigg(\frac{\mathrm{d}}{\mathrm{d}t}Z(t)\bigg)}$ je konštanta.

Deriváciou matice sa myslí derivácia po zložkách.

Zatiaľ som prišiel v a) k tomu, že dimenzia priestoru riešení systému by zrejme malo byť číslo $2nm$ , kde $m$ je počet stĺpcov matíc $X$ a $Y$ , ďalej nič.

jardofpr

ešte malá úvaha k tomu b)

za predpokladu že $X(t)$ a $Y(t)$ sú vektory dimenzie $n$ je systém tvaru

$\left[ \begin{array}{c} \frac{\mathrm{d}}{\mathrm{d}t}X(t) \\ \frac{\mathrm{d}}{\mathrm{d}t}Y(t) \end{array} \right]=\left[\begin{array}{cc} A(t) &B\\C&0 \end{array}\right] \left[ \begin{array}{c} X(t)\\Y(t) \end{array}\right]$ $(\bigstar)$

maticu tohto systému typu $2n\times 2n$ označme $E$

je vidno že $tr(E(t))=tr(A(t))+tr(0)=0+0=0$

nech $Z(t)$ je nesingulárne maticové riešenie (alebo fundamentálna matica) systému $(\bigstar)$ .

Z Liouvillovej formuly pre systémy ODR 1.rádu mám

$\frac{\mathrm{d}}{\mathrm{d}t} (\det{(Z(t))})=tr(E(t))\cdot \det{(Z(t))}$

alebo aj inak $\det{Z(t)}=C\mathrm{e}^{\int tr(E(t)) \mathrm{d}t}$

kde je z oboch zápisov vidieť, že $\det{Z(t)}=C$ pre nejakú konštantu $C$ .

Otázkou je, aký je v prípade n.m.r. $Z(t)$ vzťah medzi $\frac{\mathrm{d}}{\mathrm{d}t}\det{(Z(t))}$ a $\det{\bigg(\frac{\mathrm{d}}{\mathrm{d}t}Z(t)\bigg)}$ ,

prípadne, ak $Z(t)$ je n.m.r systému $\frac{\mathrm{d}}{\mathrm{d}t}W(t)=F(t)W(t)$ ,

či je možné systém, ktorého n.m.r. je $\frac{\mathrm{d}}{\mathrm{d}t}Z(t)$ , vyjadriť pomocou matice $F(t)$ a vektora $W(t)$ .

Potom by už zovšeobecnenie pre prípad že 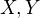$X,Y$ sú matice nebol problém.

Nejaké nápady?

EDIT: vyriešené

Matematické Fórum

#1 12. 01. 2013 16:01

maticové funkcie a systém diferenciálnych rovníc

#2 12. 01. 2013 19:29 — Editoval jardofpr (18. 01. 2013 20:47)

Re: maticové funkcie a systém diferenciálnych rovníc

Zápatí