Matematické Fórum

darkzprior · 14. 01. 2013 17:43

Ak sa zmensi pocet prvkov o 2 , zmensi sa pocet permutacii 812 krát. Urcte povodny pocet prvkov.
Tak som to ratal - 812*(n-2)!=n!
Vysli mi dva korene kvadr. rovnice - 1 a 2. Myslim ze nieco mam zle...nejake napady?

marnes · 14. 01. 2013 17:46

↑ darkzprior:

a jak vypadá ta tvá kvadratická rovnice? protože výchozí rovnice je ok

darkzprior

↑ marnes:
812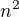 $n^{2}$ -2436n+1624=0

marnes · 14. 01. 2013 17:48

↑ darkzprior:

No tak si ji zkus vytvořit ještě jednou. Problém je nalezen

darkzprior

↑ marnes:
Aha, nasiel som chybu ale vysledok to aj tak moc nezmenilo...
$812n^{2}-2436n+1623=0$
Mozno ze tu rovnicu $812*(n-2)!=n!$ mam zle upravenu...

EDIT: po uprave mi vyslo $812=\frac{n!}{(n-2)(n-1)n!}$
potom $n!$ vykratim
a vyde mi $812=\frac{1}{n^{2}-3n+2}$
menovatel prenesem na druhu stranu a odpocitam 1
a vyde mi kvadr. rovnica $812n^{2}-2436n+1623=0$
fakt netusim co mam zle...co som videl na fore pisu ludia ze to ma mat 1 koren...