Matematické Fórum

bejf · 14. 01. 2013 22:06

Ahoj, mám příklad, který vypadá celkem jednoduše.
Řešte nerovnici s neznámou $x$ a parametrem $a\in\mathbb{R}$ .
$\frac{x-3}{x+a}\ge 1$
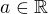Ta mi vyjde $\frac{a}{x+a}\le\frac{-3}{x+a}$ .
Podmínku si určím $x\not=-a$ .
Teď pokud $a=-3$ , tak řešením budou všechna $x\in\mathbb{R}-\{0\}$ .
Pak mám případy, kdy může být $a>-3$ nebo $a<-3$ .
Pro tyto případy budu určovat hodnoty neznámé z intervalů $(-\infty;-a), (-a;+\infty)$
A tady mé schopnosti končí. Děkuji za rady.

zdenek1 · 14. 01. 2013 22:19

↑ bejf:
$\frac{x-3}{x+a}\ge 1$
$\frac{x-3}{x+a}-\frac{x+a}{x+a}\ge 0$
$\frac{a+3}{x+a}\le 0$

a) $a>-3\ \Rightarrow\ x+a<0$
b) $a<-3\ \Rightarrow\ x+a>0$
c) $a=-3\ \Rightarrow\ x\in\mathbb R-\{3\}$

bejf · 14. 01. 2013 22:36

↑ zdenek1:
Jasně, s tou nulou jsem tam ulítnul, měla tam být trojka. Nicméně příště si to napíšu lépe, abych z toho poznal, která proměnná/parametr může nabývat jakých hodnot. Díky. :-)

Matematické Fórum

#1 14. 01. 2013 22:06

Nerovnice s parametrem

#2 14. 01. 2013 22:19

Re: Nerovnice s parametrem

#3 14. 01. 2013 22:36

Re: Nerovnice s parametrem

Zápatí