Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 01. 2013 16:03
Nerovnice s parametrem
Ahoj, mám další příklad, který bych potřeboval pomoct dotáhnout do konce.
Řešte nerovnici s neznámou  a parametrem
a parametrem 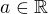 .
.

Akorát mi chybí určit x pro a>0, a<0. Vychází mi to přesně naopak, než by mělo. Nemůžu přijít v čem dělám chybu. Díky za rady.
Offline
- (téma jako vyřešené označil(a) bejf)
#2 15. 01. 2013 17:39
Re: Nerovnice s parametrem
↑ bejf:
Našel jsi řešení rovnice pro jednu hodnotu parametru.
Nerovnice má smysl, právě tehdy, když  , tedy
, tedy  . Kdyby bylo
. Kdyby bylo  , dělili bychom vlevo nulou.
, dělili bychom vlevo nulou.
Takže pro libovolné pevné 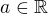 řešíme nerovnici na
řešíme nerovnici na  .
.
Ta je ekvivalentní nerovnici .
.
Rovnost může nastat pouze v případě, kdy čitatel je nula.
Zlomek vlevo je kladný, právě když nastane jedna z následujících situací:
situace čitatel jmenovatel
1) + +
2) - -
kde plus značí kladný, minus záporný.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 15. 01. 2013 18:04
Re: Nerovnice s parametrem
↑ Andrejka3:
Chápu, jen mi to nějak nevychází.
Situace 1.:
Pokud bude čitatel a jmenovatel kladný
Situace 2.:
Pokud bude čitatel a jmenovatel záporný
A teď? :-)
Mělo by vyjít:
pro a>0 
pro a<0
To mě na tom zaráží.
Offline
#5 15. 01. 2013 18:14
Re: Nerovnice s parametrem
↑ zdenek1:
Aha, já jsem si myslel, že se tam budou měnit znaky nerovnosti. Díky.
Offline


 a
a 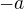 (a
(a  )
)


 )
)