Matematické Fórum

katulinka · 12. 01. 2013 00:28

Cus,

akorat jsme zacali aritmetickou posloupnost a dostali ukol

V aritmetické posloupnosti je a1=20, d=4. Kolikaty clen je roven cislo 100?

Jak to mam pocitat? Koukam na ucebnice.krynicky a vubec tu nevidim podobnej priklad resenej

Diky moc

Creatives · 12. 01. 2013 01:10

Je treba si uvedomit co je d. Potom logickou uvahou dojdes k vypoctu: $a_{1}+nd=100$ a tedy z $20+n*4=100$ vypoctu n a to bude n-ty hledany clen.

zdenek1 · 12. 01. 2013 09:06

↑ Creatives:
Pěkné, až na to, že vztah je
$a_n=a_1+(n-1)d$
$100=20+4(n-1)$

((:-)) · 12. 01. 2013 09:11 — Editoval ((:-)) (12. 01. 2013 09:15)

↑ katulinka:

Treba si uvedomiť, o čom aritmetická postupnosť je.

Podľa definície každý nasledujúci člen vznikne z predchádzajúceho pripočítaním jedného čísla (diferencie) d.

Prvý člen a1=20, d=4.

Druhý člen a2 = 20 + 4 = 24

Tretí člen a3 = 24 + 4 = 28 = 20 + 2*4

Štvrtý člen a4 = 28 + 4 = 32 = 20 + 3*4

Teda an = a1 + (n-1)*d

100 = 20 + (n - 1 )*4

Creatives · 12. 01. 2013 09:50

Jojo, sorry. Psal jsem to z postele s kapkou alkoholu v sobe hehe :P

katulinka · 13. 01. 2013 00:12

DIky moc, takze to je 21.

Mohu se jeste zeptat, jak bych resila priklad typu

4+6+8+...+x=270

zdenek1 · 13. 01. 2013 07:51

↑ katulinka:
první člen je $a_1=4$ ,
n-tý člen je $x$
a diference je 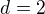$d=2$
ze vztahu
$a_n=a_1+(n-1)d$ máš
$x=4+2(n-1)\ \Rightarrow\ n=\frac{x-2}2$

Dále použijěš vztah pro součet prvních $n$ členů AP
$S_n=\frac n2(a_1+a_n)$
$270=\frac{x-2}4(4+x)$
a vyřešíš kvadratickou rovnici

katulinka · 13. 01. 2013 13:55

Takze jsem udelala

zbavila jsem se toho zlomku

1080=x^2+2x-8

Ale kdyz resim rovnici x^2+2x-1088 tak me to nevychazi, co delam spatne?

zdenek1 · 13. 01. 2013 14:15

↑ katulinka:
Rovnice $x^2+2x-1088=0$ je dobře.

co delam spatne?

Jak to mám vědět, když nenapíšeš, co s tou rovnicí provádíš?

petrik_ch · 13. 01. 2013 16:21

K precviceniu prveho prikladu:

http://www.hackmath.net/cz/priklad/578

Vedie to na jednoduchu linearnu rovnicu...

katulinka · 17. 01. 2013 10:51

Cau, diky, promin ze jsem ted neodpovidala jsme meli hodne testu ve skole a z matiky pisem az pristi tyden

Jojo, udelala jsem tam chybu koreny me vysli +32 a -34, a jako prirozene cislo de teda jen 32 takze mam vysledek 32, coz i podle vysledku je spravne.

Je tu jeste jeden priklad

Urcete soucet vsech prirozenych cisel, ktera vyhovuji nerovnici

(12x+ 2/3)*5-[(5x-15)/3]<50(x+10)

Kdyz to resim jako nerovnici tak mam kdyz se zbavim zlomku
180x+10-5x-15<150x+30

A kdyz pokracuju tak me vyjde x<1/5 (resim to stejne jako rovnici)

Ma to vyjit uplne jinak x<59 => s58=1711 -moc tomu zapisu ani nerozumim muzete me to nekdo prosim trochu objasnit?

jelena · 17. 01. 2013 23:58

↑ katulinka:

Zdravím,

nalezeno při úklidu - pro nové dotazy je lepší si zakládat nové téma viz pravidla.

Řekla bych, že zde jsou chyby: 180x+10-5x-15<150x+30 (ještě si překontroluj - pokud nepomůže, tak do nového tématu). Děkuji.

Matematické Fórum

#1 12. 01. 2013 00:28

Aritmeticka posloupnost - zacatek

#2 12. 01. 2013 01:10

Re: Aritmeticka posloupnost - zacatek

#3 12. 01. 2013 09:06

Re: Aritmeticka posloupnost - zacatek

#4 12. 01. 2013 09:11 — Editoval ((:-)) (12. 01. 2013 09:15)

Re: Aritmeticka posloupnost - zacatek

#5 12. 01. 2013 09:50

Re: Aritmeticka posloupnost - zacatek

#6 13. 01. 2013 00:12

Re: Aritmeticka posloupnost - zacatek

#7 13. 01. 2013 07:51

Re: Aritmeticka posloupnost - zacatek

#8 13. 01. 2013 13:55

Re: Aritmeticka posloupnost - zacatek

#9 13. 01. 2013 14:15

Re: Aritmeticka posloupnost - zacatek

#10 13. 01. 2013 16:21

Re: Aritmeticka posloupnost - zacatek

#11 17. 01. 2013 10:51

Re: Aritmeticka posloupnost - zacatek

#12 17. 01. 2013 23:58

Re: Aritmeticka posloupnost - zacatek

Zápatí