Matematické Fórum

exrebok · 18. 01. 2013 21:32

Zdravím,

Chcel by som sa opýtať, že ako aplikujem na túto funkciu L hosp. pravidlo.

$\lim_{x\to3} (3-x).\text{tg}\frac{\pi x}{6} = \parallel \infty \parallel =$

sa to rovná nekonečnu. A kedže L hosp. pravidlo môžem aplikovať iba keď ide o tvar: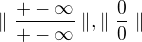

$\parallel \frac{+-\infty }{+-\infty }\parallel , \parallel \frac{0}{0} \parallel$

A neviem ako dostanem požadovaný tvar. Hoci ma napadlo že 1= x/x .... a to potom derivujem, len mi to nejak divne vychádza.

standyk · 18. 01. 2013 21:36

↑ exrebok:

Ahoj, skús si rozpísať ten tangens...

exrebok · 18. 01. 2013 23:07

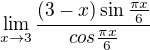spravil som to vyšlo mi z toho: $\lim_{x\to3} \frac{(3-x)\sin \frac{\pi x}{6}}{cos \frac{\pi x}{6}}$ .... môžem použiť L hosp. pravidlo pre x sa blíži k 3 z ľava(interva: $x\in (-\infty ,3)$ ) , dostanem niečo takéto:

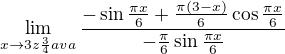$\lim_{x\to3 z ľava} \frac{-\sin \frac{\pi x}{6}+\frac{\pi (3-x)}{6}\cos \frac{\pi x}{6}}{-\frac{\pi }{6}\sin \frac{\pi x}{6}}$ a teraz nvm čo mam s tým robiť ale vôbec O.o