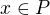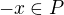Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 01. 2013 13:21 — Editoval Andrejka3 (19. 01. 2013 13:30)
Re: uspořádané pole
↑ Honza90:
Dobrý den.
Je to poněkud málo, myslím. Měly by tam být nějaké podmínky, že se tato množina chová nějak hezky vůči operacím pole, řekla bych.
Poslední podmínka nemá být spíše 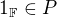 ?
?
Aspoň dám odkaz: Wikipedia
Edit:  je pole, že? Pak bych mohla říct,
je pole, že? Pak bych mohla říct,  a splňuje tvou podmínku.
a splňuje tvou podmínku.  a
a 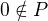 .
.
Ale pak  a
a  a
a  z monotonie sčítání. Máme cyklus.
z monotonie sčítání. Máme cyklus.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 19. 01. 2013 13:28
Re: uspořádané pole
↑ Andrejka3:
ano, musí platit  a
a 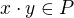 pro
pro 
Když se na to tak dívám, tak bych řekl, že 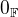 tyto podmínky nijak neporušuje.
tyto podmínky nijak neporušuje.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#4 19. 01. 2013 13:33 — Editoval Andrejka3 (19. 01. 2013 13:39)
Re: uspořádané pole
↑ Honza90:
Aha, já nepochopila otázku :)
Kdyby byla 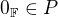 , pak by
, pak by  , což nastat nemůže.
, což nastat nemůže.
Edit: Nebo stále nechápu otázku?
Prostě, celá množina se rozdělí na kladnou část (P), zápornou část (-P) a nulu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 19. 01. 2013 13:55
Re: uspořádané pole
↑ Andrejka3:
Souhlasím, jenže v jedněch skriptech se píše, že tam nula patří. Zase proč by jinak nemohla, operace 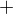 i
i  budou na
budou na  uzavřené i když v P bude nula.
uzavřené i když v P bude nula.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#8 19. 01. 2013 14:05
Re: uspořádané pole
Zatím si myslím, že by se nic nezměnilo, jen by se musela přeformulovat definice na začátku - alespoň jedna z následujících možností.
Definuje se uspořádání na 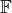 tak, že
tak, že  . Takhle by stačilo takto definovat neostré uspořádání, zatím nevidím v tom problém.
. Takhle by stačilo takto definovat neostré uspořádání, zatím nevidím v tom problém.
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 19. 01. 2013 15:00
Re: uspořádané pole
↑ Andrejka3:
Kdybychom přeformulovali tu definici na začátku, pak nedostaneme to kýžené disjunktní rozdělení - každý nenulový prvek je kladný anebo záporný. Takže si myslím, že to má spíše význam ten, že se dá napsat ta definice snadno.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 19. 01. 2013 15:14
Re: uspořádané pole
↑ Andrejka3:
Konečná pole nelze uspořádat.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#11 19. 01. 2013 15:22 — Editoval Andrejka3 (19. 01. 2013 16:54)
Re: uspořádané pole
↑ Honza90:
Ano, jistě. Dá se do nich vnořit  (do těch uspořádaných).
(do těch uspořádaných).
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 19. 01. 2013 19:30
Re: uspořádané pole
↑ Andrejka3:
To vnoření mi trochu přibliž, prosím.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline
#13 19. 01. 2013 20:26
Re: uspořádané pole
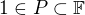 , protože
, protože 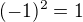 , takže kdyby
, takže kdyby 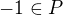 , máme spor.
, máme spor. , pro
, pro 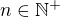 .
.
Když si označím 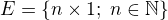 , je tato struktura s + a násobením tělesa a uspořádáním (restrikcemi) izomorfní komutativnímu monoidu
, je tato struktura s + a násobením tělesa a uspořádáním (restrikcemi) izomorfní komutativnímu monoidu 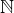 přirozených čísel s obvyklým sčítáním, násobením a uspořádáním.
přirozených čísel s obvyklým sčítáním, násobením a uspořádáním.
Definice 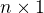 lze přirozeně rozšířit na
lze přirozeně rozšířit na  ,
, 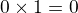 ,
, 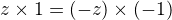 pro
pro  záporné. Příslušná množina
záporné. Příslušná množina  je pak s restrikcemi operací a uspořádání izomorfní uspořádanému oboru integrity
je pak s restrikcemi operací a uspořádání izomorfní uspořádanému oboru integrity 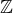 celých čísel.
celých čísel.
Mějme 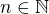 .
.
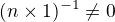 . Z monotonie na nasobeni kladnymi prvky plyne, ze se relace zachova po vynasobeni
. Z monotonie na nasobeni kladnymi prvky plyne, ze se relace zachova po vynasobeni 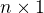 , takze
, takze  . Odtud je asi vidět, jak definovat
. Odtud je asi vidět, jak definovat  a jak dostat strukturu izomorfni s
a jak dostat strukturu izomorfni s  .
.
What does a drowning number theorist say?
'log log log log ...'
Offline

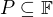 a pro
a pro 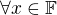 platí právě jedna z možností:
platí právě jedna z možností: